2D衝突編
その14 楕円と点の最短距離
先日同僚から「楕円と点の最短距離を求める方法って無いですかね?」と尋ねられました。最初「楕円をスケールして円にして最短点を求めてスケールを元に戻したら?」と思ったのですが、これは正しく無い事がすぐに判明。そこで真面目に解いてみる事にしました。ちなみに、中々のいばら道です(-_-;
① まずは楕円を標準化
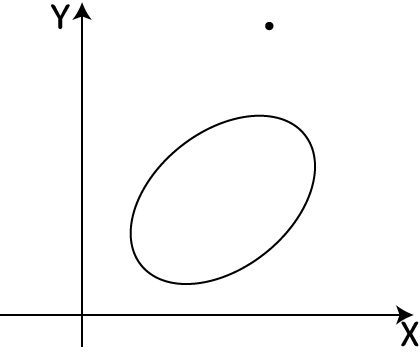
楕円と点が下の図のようにあるとします:
今欲しいのは点から楕円までの最短距離となる楕円上の点です。ただ上の図の状態だと考えるのがとても難しくなってしまいますので、楕円を標準化(長短軸をXY軸に合わせる)する所から始めます。
多くの場合、上のような楕円は「元の標準楕円を回転させてオフセット」みたいな作業で描かれます。その回転角度をα、オフセット量を(Ox, Oy)とすると、楕円は逆オフセットした後に逆回転する事で標準楕円に戻ります。これを点にも適用すると楕円との位置関係はそのままで下図のような少し分かり良い状態になります:
元の点をQ'とするなら、Q'をQに変換する式は逆オフセットと逆回転をすれば良いので、
と算出できます。逆オフセット行列と逆回転行列をこの順番に掛け算して整理しただけです。これで準備が整いました。
② 楕円の法線上に点Qがある
上に標準化した楕円、それと位置関係を共にする点Qを再掲しました。点Qから楕円までの最短距離は、楕円上の点Pから伸ばした法線Nを方向とする線分PQの長さdに他なりません。よってそういう条件になる点Pを求めるのが今回のゴールです。
楕円はX軸側の長径の長さをa、Y軸側の短径をbとします。この時楕円は以下の極座標で表現出来ます:
今欲しいのは点Pでの法線ベクトルNです。これは点Pでの接線ベクトルTと直行するベクトルです。点Pでの接線ベクトルTは上の極座標を双方θで微分すると求まります:
xがちょっと進んだ時にyがどれだけ進むかが接線ベクトルですから、上式のようになる訳です。法線はこの接線ベクトルTと垂直関係にあります。2Dベクトルの場合、それを垂直にするにはX成分とY成分を入れ替えて、どちらかの符号を反転すればOKです。つまり、
これがあるθで求められる点Pでの法線ベクトルの式となります。すこぶるシンプル(^-^)
③ 点Pから伸びる直線上の点Q
上式から、とあるθがあれば点Pがわかり、その点Pでの法線ベクトルNも計算できることが分かりました。この点Pから伸びる直線上に点Qがあれば、その線分PQの長さが最短距離となります。
点Pから法線Nの方へ延びる直線上の点Qは、
と表現出来ます。tは何らかの係数です。適切な点Pであれば、tをうまく調整すると法線ベクトルが伸び縮みしてうまい事点Qに辿り着くというわけです。今点Qは既知で、点Pと法線Nはθで表される事が分かっています。上の式にそれらを代入すると、
X成分Y成分それぞれcosθとsinθでまとまった連立方程式が出来上がりました。ここからθを消します:
(cosθ)^2 + (sinθ)^2 = 1を利用してθを消すと、最下段のようなtの4次方程式がお目見えします。t(実数解)が最大で4種類あるという事、つまり円周からその法線方向に点Qに向かって伸びる直線の候補が最大4本存在する、という事です。例えば点Qが原点にある時は上下左右に点Pが4つあるのがイメージできますよね。多くの場合は2本(重解が1つと虚数解が2つ)かなと思います。今回の問題を解決するにはこの4次方程式を解かなければならないのです。これがまたいばら道なのです…(-_-;
④ 4次方程式の解の公式
2次方程式に解の公式があるように、実は4次方程式にも解の公式が存在します。その公式に各次数の係数を放り込めば解が求まります。幾つか表現がありますがここではフェラーリの方法を採用する事にします(Wikipedia:4次方程式参照)。
以下Wikipediaの受け売りではありますが、③まで出てきた記号で示し直します。まず③の最後に求めた4次方程式の左辺をt^4の係数で割り算して4乗項の係数を1に整理します:
t^4以外の各係数をA,B,C,Dとしてまとめる事で最下段のようにコンパクトになります。
ここから方程式を解くため変数変形をして3乗項を無くしてしまいます。
という変数を用意して上式に代入すると、
3乗項が消えました。見やすくするためこれを、
と書き直しておきます。
ここでもしq = 0(多分円の場合)であったら、上の式はh=s^2とすると2次方程式に帰着するので、そのまま解く事が出来ます:
興味があるのは実数解のsなので、2次方程式の判別式を使って虚数解になる物は省きます。図形的に楕円上には必ず最近点が存在するので、sが虚数解のみになる(4次方程式が実数解を持たない)事はありません。
q = 0は幸せパターンですが、多くの場合qはゼロ以外の値になります。その時は真面目に4次方程式を解く作業となります。そのために唐突ですが以下のような式を持ち出してそれを展開してみます:
先の式と見比べると、rの部分がp,q,uで表現されている事が分かります。「等価的に等しい」というやつです。よって、
というuについての3次方程式が出てきます。なぜこんなことをしているかというと、唐突に持ち出した先の式は高校の最初の方で習った2次の値同士の引き算の因数分解の式の形になっていて、
このように括弧の中がそれぞれsの2次方程式になっている因数分解ができるんです。この方程式を満たすには、各2次方程式をsについて解けば良いんです。p,qは既知の係数ですから、後はuの値さえ分かれば簡単に解けます!そのためにuの3次方程式を導いた…という事なんです。フェラーリさん、凄い事を考えるもんです!
ただ…えーと、今度はuの3次方程式を解く必要がある訳でして、苦難は続きます…。
⑤ 3次方程式の解の公式
3次方程式にも解の公式が存在します。これもWikipediaにまとめられていますが、流れとしては最初に式変形をして2次の項を消し去ります。その後は「カルダノの公式」もしくは「ビエタの公式」へとつなげ解を求めます。ビエタの公式は方程式が3つの実数解もしくは重解を持つ場合に用いる事が出来ます。式が簡単なのでなるべくならこちらを使いたいのですが、1つの実数解と2つの虚数解の場合には適用できないので、この時だけカルダノの公式を使う事にします。
まずは2次の係数の消去の仕方です。④のuの3次方程式を展開します:
ここでuを、
と置き換えて上式に代入すると、
このように2次の項が無い簡易型の3次方程式に変換できます。この係数もf,gでまとめて見た目をすっきりさせておきましょう:
ここから「カルダノの公式」を使うか「ビエタの公式」を使うか判別式で判断します。上の形の場合判別式はとてもシンプルで、
と計算して、D>0なら3実数、D=0なら重解、D<0なら1実数2虚数解となります。
D>=0の場合はビエタの公式を使えます。
と置き換えるとこのmとnを用いてvは、
と解く事が出来ます。手計算では太刀打ち行きませんが、数値計算ならば大変シンプルに解が求まります。ただし、先程も示しましたがこれはあくまでも実数解のみの場合です。
判別式D<0の時は虚数解が存在するので以下のカルダノの公式を用います:
v0,v1,v2が求まる3つの解です。ωはx^3=1の解の虚数解です。D<0の時は実数解が1つと虚数解が2つになりますが、ここでも感心があるのは実数解のみです。ただ、だからと言って虚数であるω1とω2が掛け算されていないv0が実数解になるわけではありません(ここ注意!)。上式でv0はルート内がマイナスだと虚数解になりますし、v1,v2で虚数同士が掛け算されて虚数項が無くなってしまうパターンは至って普通にあります。なのでv0,v1,v2はどれも計算が必要です。
ビエタの公式やカルダノの公式で実数解vが求まると、
からuが求まり、そのuから、
のパラメータが全部定まります。両方の括弧とも2次方程式なので、2次の解の公式で簡単にsが求まります。で、sが求まると、
から法線ベクトルを点Qまで引き延ばすtが求まります。tからはcosθ、sinθの値が、
で逆算されます。ただ点QのX成分やY成分がゼロの時にはスケールが失われる事があるので、有効な数字が入っている方を採用した方が良い感じになります:
Sgnは符号判定です。マイナスなら-1.0、プラスなら+1.0が返ります。
最終的に求めたい長さLは、
で求まります。ただしtは最大4つ実数解が存在しますので、算出されてきた実数解すべてにおいてLを計算します。その中で一番短いLが今回求めたかった最短距離となります!
⑥ 楕円と点との最短距離を求める関数
さて、では⑤までの理屈をコードに落とします。大変だぞぉ…(これから実装する自分へ言い聞かせてますw)。入力するパラメータは楕円のX軸側径aとY軸側径b、そして点の座標(Qx, Qy)だけです:
#include <complex> // 複素数計算の為に必要
#include <math.h>
#include <float.h>
// -1~1クランプ
double clamp( double v ) {
if ( v < -1.0 ) {
v = -1.0;
}
else if ( v > 1.0 ) {
v = 1.0;
}
return v;
}
// 2次方程式の解を算出
// a,b,c : 係数
// solves: 解
void solv2Equation( const std::complex< double > &a, const std::complex< double > &b, const std::complex< double > &c, std::complex< double > solves[ 2 ] ) {
solves[ 0 ] = ( -b + sqrt( b * b - 4.0 * a * c ) ) / ( 2.0 * a );
solves[ 1 ] = ( -b - sqrt( b * b - 4.0 * a * c ) ) / ( 2.0 * a );
}
// 複素数の立方根を算出
std::complex<double> cubicRoot( const std::complex<double> &val ) {
double d = pow( abs( val ), 1.0 / 3.0 );
double r = arg( val ) / 3.0;
return std::complex<double>( d * cos( r ), d * sin( r ) );
}
// 算出されたtから最短距離となる点Pを算出
bool calcMinDistPoint( double x, double y, double a, double b, int solveNum, const std::complex< double > *ts, double eps, double &px, double &py, double &dist ) {
dist = FLT_MAX;
for ( int i = 0; i < solveNum; ++i ) {
// 実数解のみを選別する
const std::complex< double > t = ts[ i ];
if ( abs( t.imag() ) > eps || abs( a + t * b ) < eps || abs( b + t * a ) < eps ) {
continue;
}
double cos = clamp( x / ( a + t.real() * b ) );
double sin = clamp( y / ( b + t.real() * a ) );
if ( abs( cos ) > abs( sin ) ) {
sin = sqrt( 1.0 - cos * cos ) * ( sin >= 0.0 ? 1.0 : -1.0 );
}
else {
cos = sqrt( 1.0 - sin * sin ) * ( cos >= 0.0 ? 1.0 : -1.0 );
}
double nx = b * cos * t.real();
double ny = a * sin * t.real();
double L = sqrt( nx * nx + ny * ny );
if ( L < dist ) {
dist = L;
px = a * cos;
py = b * sin;
}
}
return ( dist != FLT_MAX );
}
// 楕円と点との距離を算出
// xLen : 楕円のX軸方向の径の長さ
// yLen : 楕円のY軸方向の径の長さ
// x,y : 点の座標
// dist : (出力)最短距離
// px,py: (出力)最近接点
// 戻り値: 最短距離が求まった場合はtrue、最短距離が存在しないなど不正の場合はfalse
bool distEllipsePoint( double xLen, double yLen, double x, double y, double &dist, double &px, double &py ) {
xLen = ( xLen < 0.0 ? 0.0 : xLen );
yLen = ( yLen < 0.0 ? 0.0 : yLen );
// 楕円が縮退している場合は線分との距離になる
if ( xLen == 0.0 ) {
double dy = abs( y ) - yLen;
if ( dy > 0.0 ) {
dist = sqrt( x * x + dy * dy );
return true;
}
dist = abs( x );
return true;
}
if ( yLen == 0.0 ) {
double dx = abs( x ) - xLen;
if ( dx > 0.0 ) {
dist = sqrt( y * y + dx * dx );
return true;
}
dist = abs( y );
return true;
}
// パラメータ(マルペケの記事参照の事)
const double a = xLen;
const double b = yLen;
const double a2 = a * a;
const double b2 = b * b;
const double x2 = x * x;
const double y2 = y * y;
const double A = 2.0 / ( a * b ) * ( a2 + b2 );
const double B = 4.0 + ( a2 - x2 ) / b2 + ( b2 - y2 ) / a2;
const double C = 2.0 / ( a * b ) * ( a2 + b2 - x2 - y2 );
const double D = 1.0 - x2 / a2 - y2 / b2;
const double E = A / 4.0;
const double p = B - 6.0 * E * E;
const double q = C - 2.0 * B * E + 8.0 * E * E * E;
const double r = D - C * E + B * E * E - 3.0 * E * E * E * E;
const double alpha = 2.0 * p;
const double beta = p * p - 4.0 * r;
const double gamma = -q * q;
const double f = beta - alpha * alpha / 3.0;
const double g = gamma - alpha * beta / 3.0 + 2.0 / 27.0 * alpha * alpha * alpha;
static const std::complex< double > w1 = std::complex< double >( -0.5, sqrt( 3.0 ) / 2.0 ); // x^3 = 1の虚数解ω1
static const std::complex< double > w2 = std::complex< double >( -0.5, -sqrt( 3.0 ) / 2.0 ); // x^3 = 1の虚数解ω2
static const double eps = 0.00000000001;
// q=0の時の特殊ケース
// 多分、円の場合
if ( abs( q ) < eps ) {
int solveNum = 4;
std::complex<double> h[ 2 ] = {};
solv2Equation( 1.0, p, r, h );
std::complex<double> ts[ 4 ] = {};
ts[ 0 ] = sqrt( h[ 0 ] ) - E;
ts[ 1 ] = -sqrt( h[ 0 ] ) - E;
ts[ 2 ] = sqrt( h[ 0 ] ) - E;
ts[ 3 ] = -sqrt( h[ 0 ] ) - E;
// 最近接点を算出
return calcMinDistPoint( x, y, a, b, solveNum, ts, eps, px, py, dist );
}
std::complex< double > v[ 3 ]; // パラメータvの解
const double adjD = -4.0 * f * f * f - 27.0 * g * g; // 判別式
if ( adjD >= 0.0 ) {
// 実数解のみなのでビエタの公式利用
double m = sqrt( -f / 3.0 );
double n = -g / m / m;
for ( int j = 0; j < 3; ++j ) {
double np2m = clamp( n / ( 2.0 * m ) );
v[ j ]._Val[ 0 ] = 2.0 * m * cos( 1.0 / 3.0 * acos( np2m ) + j * 2.0 / 3.0 * 3.14159265358979323846 );
}
}
else {
// 実数解1、虚数解2なのでカルダノの公式利用
std::complex< double > rt = sqrt( pow( g / 2.0, 2.0 ) + pow( f / 3.0, 3 ) );
std::complex< double > L = std::complex< double >( -g / 2.0, +0.0 ) + rt;
std::complex< double > R = std::complex< double >( -g / 2.0, -0.0 ) - rt; // +0.0, -0.0の符号明記はcubicRoot関数内で回転方向を決めるので重要!
std::complex< double > CL = cubicRoot( L );
std::complex< double > CR = cubicRoot( R );
v[ 0 ] = CL + CR;
v[ 1 ] = w1 * CL + w2 * CR;
v[ 2 ] = w2 * CL + w1 * CR;
}
// 4次方程式を解いて法線ベクトルのスケールとなるtを算出
std::complex< double > ts[ 12 ] = {};
int solveNum = 0;
for ( int i = 0; i < 3; ++i ) {
std::complex< double > solves[ 4 ];
std::complex< double > u = v[ i ] - alpha / 3.0;
solv2Equation( 1.0, -sqrt( u ), ( p + u ) / 2.0 + q / ( 2.0 * sqrt( u ) ), solves );
solv2Equation( 1.0f, sqrt( u ), ( p + u ) / 2.0 - q / ( 2.0 * sqrt( u ) ), solves + 2 );
ts[ solveNum ] = solves[ 0 ] - E;
ts[ solveNum + 1 ] = solves[ 1 ] - E;
ts[ solveNum + 2 ] = solves[ 2 ] - E;
ts[ solveNum + 3 ] = solves[ 3 ] - E;
solveNum += 4;
}
// 最近接点を算出
return calcMinDistPoint( x, y, a, b, solveNum, ts, eps, px, py, dist );
}
今回は複素数計算が入るためcomplexを多用しています。またその為にdouble型で統一しています。最近のFPUはfloatをdoubleで計算するので、普通のPCを使っているなら特に問題ありません(^-^;。
distEllipsePoint関数が本丸です。引数の意味はコメントの通りで、distに最短距離が、px,pyに最近接点の座標が返ります。複素数の3乗根はpow(v, 1.0 / 3.0)で通常計算できるのですが、今回は解を正しく求めるためにcubeRoot関数を設けました。ここ、死ぬ程ハマった所です(-_-;;。複素数でpow使うの怖くなりました。
大分テストはしましたが、もし挙動におかしなところがありましたらご連絡頂けると嬉しいです(誰がこの関数使うんだって話もありますが(^-^;;)