2D衝突編
その5 円と線分から多角形と円へ
多角形は線で構成された閉じた図形です。多角形と円が衝突しているかどうかを判定できれば、複雑な形状をしたものと球とを正しく衝突判定させる事ができるようになります。効率はあまり良くありませんが、知って損はありません。
ひとつ注意。ここでの多角形は「凸多角形(多角形のどの内側の角度も180度以下である多角形)」です。凹多角形だとうまくいきません。
① 多角形の定義
まず多角形を定義します。記号化がちょっと面倒なのですが、配列のような書き方にしておきます:
多角形 : 頂点P[n](x[n], y[n])
円は言わずもがなですが、中心点の座標と半径で定義できます:
円 : 中心点C(xc, yc)、半径r
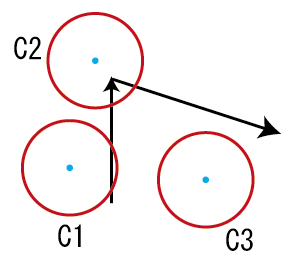
では下の図を御覧ください:
この図は多角形の一部と幾つかの衝突を起こしている円の状態を示しています。C1とC2は多角形の外側で衝突していますし、C3に至っては完全に含まれています。C3はちょっと特殊なんですが、C1、C2については「多角形の一辺(線分)と円の中心点の距離が円の半径よりも短い」ために衝突しています。つまり、円と線分の距離がわかればC1やC2は対処できます。
② 円と線分の衝突
円と線分との衝突は、円の中心点から線分までの距離で判定することができます。下の図を御覧ください:
線分の両端のどちらかを始点、他方を終点とし、視点から終点へ向かうベクトルSを定義します。また視点から円の中心点P、及び終点からPへ伸びるベクトルをそれぞれA、Bと定義します。中心点から線分までの距離は上図のdです。
中心点Pと線分までの距離dは、三角関数を用いると、
d = |A|・sinθ
ですね。ここで基礎の基礎編その1「内積と外積の使い方」の③にある外積に注目です。外積の式は次のようでした:
v1×v2= x1*y2-x2*y1 = |v1||v2|sin(θ)
式中のv1をベクトルS、v2をベクトルAとすると、上式はこうなります:
S×A= |S||A|sin(θ)
この両辺を|S|で割ると、右辺は先の距離dの求め方の右辺と全く一緒になります。つまり、距離dは
d = |S×A| / |S|
となります。この距離dが円の半径rより大きければ、どう頑張っても円は線分に接しないので判定をそこで終わらせます。
d ≦rの場合、円は線分に衝突している可能性があります。「可能性がある」というのは、以下のような例外があるからです:
上図のように、円の中心点が線分の両端の外側にある場合、距離dが半径よりも短くても線分と衝突しない場合があります。これを見つけるには、上図のθ1とθ2が両方共鈍角である事を調べればOKです。θの符号はcosθで間接的に知る事が可能です。θが90度よりも大きくなればcosθはマイナスになります。そして、cosθの値はベクトルの内積で即座に計算できるのでした。よって、図内に示しているようにベクトルAとS、ベクトルBとSの内積をそれぞれ求めて掛け算し、それがプラスならば上図のような例外になっていると判定できます。
例外の場合は線分の両端のどちらかと衝突する可能性がありますから、ベクトルAやベクトルBの長さが半径rよりも短ければ衝突しています。
以上をまとめると、
○ d ≦ rの時
・ Dot(A, S) * Dot( B, S ) ≦ 0 →衝突
・ ↑では無い例外の場合、r > |A| or r > |B|なら衝突
と整理されます。
③ 多角形と円の衝突
②で示した一連の作業を多角形を構成するすべてのベクトルについて行えば、線分と交わっているパターンはクリアできます。多角形の内側に完全に含まれる円については、「その4」でも触れましたが、円の中心点がすべてのベクトルから見て右側にあるかをチェックすれば良いだけです。
多角形と円の衝突についてまとめます。
多角形の頂点 P[n](xp[n], yp[n]) (時計回りに定義)
多角形を構成するベクトルV[n]=(vx[n], vy[n])
円の中心点 C(xc,yc)
円の半径 r
多角形の頂点から円の中心点へ向かうベクトル M[n]=(Mx[n], My[n])
① 線分の内側?
V[n]・M[n]≧0(鋭角)且つV[n]・M[n+1]≦0(鈍角)で|V[n]×M[n]|/|V[n]|≦rならば衝突を起こしている。
② 線分の外側の例外ケース
①ではない時、(xc-xp[n])^2+(yc-yp[n])^2≦r^2もしくは(xc-xp[n+1])^2+(yc-yp[n+1])^2≦r^2ならば衝突を起こしている。
③ ①と②がすべての辺で成り立っていない時に、V[n]×M[n]≦0(線分の右側に頂点がある)がすべての辺について言えるなら衝突を起こしている。
ちょっと複雑ですが、個々のプロセスは特に難しい事をしている訳ではありません。