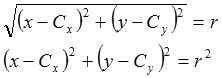
3D衝突編
その17 スクリーンカーソルで境界球の表面を指す
ゲームではしばしスクリーン上にあるカーソルで画面内のモデルを指し示す場面が登場します。この時、対象キャラクタを境界球で包んでいたとしましょう。
カーソルはスクリーン座標です。一方で画面内のモデルはビュー空間にいます。よって、スクリーン座標のある点をビュー空間に戻す必要があります。さらに、境界球の表面の座標をしっかり触る必要もあるかもしれません。その場合、画面から境界球に向けてレイを飛ばし、その交点を求める必要があります。
この境界球の表面をジャストミートで指し示すにはどういう計算が必要になるか?この章ではそんな事を試行錯誤してみたいと思います。
① 画面の奥へレイを飛ばすというのは
ゲーム画面の奥へレイを飛ばすというのは、見た目は簡単ですが実はちょっと奥深いものがあります。ローカルにあるモデルが見た目の画面、つまりスクリーンまで届くには、ワールド変換行列、ビュー行列、射影変換行列そしてビューポート行列という実に4つの行列を経る必要があります。逆に言えば、スクリーン上のある点はこれらの逆行列を逆順に掛けていく事でモデルのローカル空間にまで戻す事もできるわけです。ただ、スクリーン座標は2Dであるため、Z座標の情報は欠落します。
そこで、スクリーン座標にZ成分0.0f及び1.0fを付け加えます。そしてz=0.0fの点から1.0fの点に向けてベクトルを伸ばします。これが「画面の奥へのレイ」になるわけです。そして、この2点に対して先の変換行列の逆行列を掛けていくことで、色々な空間でレイを飛ばす事ができるようになります。
ただ、欲しい境界球表面の座標は、ワールド空間にあります。では、ワールド空間で交点を求める必要があるのか・・・というと、必ずしもそうする必要はありません。例えば射影空間で求めた交点は、ビュー逆行列とワールド変換逆行列を掛ける事で、ワールド空間に戻す事ができます。つまり、「交点はどこの空間で求めても構わない」という事です。
であるならばです。どの空間で求めても構わないのであれば計算が簡単な空間で求めたいですよね。どの空間だと計算が簡単になるのでしょうか?
まずスクリーン座標はどうでしょう?この座標空間で嬉しいのは、レイの方向がZ軸と平行になる点です。しかし、境界球のZ軸スケールは0.0〜1.0という狭い範囲に縮んでしまっています。これだと、球が球でなくなっているため、計算が恐ろしく面倒になります。スクリーン座標は駄目そうです。同じ性質が射影空間にもありますから、射影空間も難しいですね。
ではビュー空間はどうでしょう?この空間はカメラの目線で世界を見ています。つまり、スクリーン空間の座標の軸と各軸が平行になっています。そして、嬉しい事にこの空間では境界球はゆがんでいません。ただし、レイの方向はもはやZ軸と平行にはなりません。ゆがんでいない境界球に斜めに走るレイを飛ばして交点を得る。そういう計算が必要です。ワールド空間でもローカル空間でも状況は同じです。
となると、結局の所レイをワールド空間にまで戻すのが良さそうです。本章の問題は、ワールド空間にある境界球に任意のレイを飛ばして交点を得るという問題に帰結しました。
② 境界球の表現
境界球は半径rと中心の位置p(ワールド空間上)で表現されます。一方レイは始点sと終点eのある方向性を持った線分です。この交点を求めてみましょう。
交点を求めるには式が必要です。線分ならy=ax+bとかax + by + c = 0などと表現されますね。では「球」はどう式で表現されるのか?・・・と、微妙にわかるようなわからないような・・・(^-^;。そこで、まずは円で考えてみましょう。
円と言うのは「2D上においてある点Cから等しい距離にある点Pの集合」です。中心点に当たる固定点Cを(Cx, Cy)、円の条件を満たす変数点Pを(x, y)とすると、両者の距離は、
となります。上の式が直接的です。下の式はいわゆるピタゴラスの定理ですよね。さて、上式をじ〜〜〜っと見ます。そしてこんな風に書いてみます:
Q=P-Cというベクトルです。面白い事に、円の式というのは「ベクトルの内積」で表現できてしまうんですね。
さて、これを踏まえて球の式を考えます。球というのは「3D上においてある点Cから等しい距離にある点Pの集合」です。円と概念は一緒で、2Dが3Dになっただけです。中心点に当たる固定点Cを(Cx, Cy, Cz)、球の条件を満たす変数点Pを(x, y, z)とすると、両者の距離は・・・って、円と全く同じ文言ですよね。結局、次元が大きくなっただけで、上の性質は全く持って一緒。つまり、球の式は、
とやっぱり内積で表現できてしまいます。
③ 境界球と線分の交点
境界球の表現は良さそうです。一方の線分(レイ)も、
と表現できます。Sはレイの開始点(3D上の点です)、Vはレイの方向を現す単位ベクトル(=長さが1)で、tは数値です。tの値を色々に変えると、例の上の任意の点R(t)を表す事ができるわけです。
さて、境界球と線分が交わる時、両者には「共通点」が存在します。球の条件を満たすのは点Pでした。衝突点はこの点Pのどれかで、その点はレイ上にもあるわけですから・・・境界球の点PをR(t)に置き換えられます。すると、:
と、なんと2次式が出現します!ここでU = S-C、a=Dot(V,V)=1(Vが単位ベクトルなので)、b=Dot(U,V)そしてc=Dot(U,U)-r^2です。これを解いた時のtが、衝突点を表してくれるわけです。
tを解くのは極めて簡単で、いわゆる解の公式を使います:
すげー簡単になりました(^-^)。こうして求めたtをR(t)に代入すれば、めでたく交点が算出されます。
④ 解の存在と交点の関係
薄々おわかりになるかとは思いますが、tは存在しない事があります。境界球とレイが交差しない時です。またtが重複解を持つ事もあります。これは球とレイが接した場合です。レイが球に突き刺さる時は刺さって抜けるので必ず2点と衝突します。
2点のうち最初に接するのは、tが小さいほうです。tがマイナスの場合もありますので注意して下さい。tがマイナスという事は、レイの開始点Sの後ろで貫通するという事です。無限レイであればそれでもOKですが、有限の場合は捨てる必要があります。
⑤ 球とレイの交点算出関数
ここで球とレイの交点を算出する関数を公開致します:
球とレイの交点算出関数 #define IKD_EPSIRON 0.00001f // 誤差
///////////////////////////////////////////////////
// 球と無限レイの衝突判定
// r : 球の半径
// center : 球の中心点
// s : レイの開始点
// v : レイの方向ベクトル
// pOut_colli : 衝突位置
// pOut_t : 衝突時刻(出力)
// 戻り値 : 衝突(true), 非衝突(false)
bool CalcSphereRayCollision(
float r,
D3DXVECTOR3* center,
D3DXVECTOR3* s,
D3DXVECTOR3* v,
D3DXVECTOR3* pOut_colli,
float* pOut_t
) {
D3DXVECTOR3 u = *s - *center;
float a = D3DXVec3Dot( v, v );
float b = D3DXVec3Dot( v, &u );
float c = D3DXVec3Dot( &u, &u ) - r * r;
if ( a - IKD_EPSIRON <= 0.0f ) {
// 誤差
return false;
}
float isColli = b * b - a * c;
if ( isColli < 0.0f ) {
// 衝突しない
return false;
}
float t = ( -b - sqrt( b * b - a * c ) ) / a;
if ( pOut_t ) {
*pOut_t = t;
}
if ( pOut_colli ) {
*pOut_colli = *s + *v * t;
}
// 衝突している!
return true;
}
ご自由にお使い下さい。は〜終わった・・・でなかったですね。スクリーン上から球を指さないといけないのでした(^-^;
⑥ スクリーン座標をワールドへ
スクリーン座標をワールドへ持っていくためには、境界球のワールド変換行列(大抵モデルのそれ)、ビュー行列、射影変換行列そしてビューポート行列が必要です。これらはすべて既知だとしましょう。
ビューポート行列は普段ユーザが定義しない事も多いかと思います。これは描画デバイスから間接的に取得できます。間接的というのは行列の形ではなくてD3DVIEWPORT9構造体として取得できるためです。これを行列の形に整えます。ビューポート行列自体はDirectXのマニュアルにも掲載されています(Viewports and Clipping (Direct3D 9))。
スクリーン座標をワールド空間へ写像する実装は次のような感じになります:
スクリーン座標をワールド空間へ変換 ///////////////////////////////////////////////////
// スクリーン座標をワールド座標へ変換
// out : ワールド座標(出力)
// pDev : 描画デバイス
// sx, xy : スクリーン座標
// z : スクリーン座標の仮想的なZ成分(0.0〜1.0)
// view : ビュー行列
// proj : 射影変換行列
// 戻り値 : ワールド座標(出力)
D3DXVECTOR3* transScreenToWorld(
D3DXVECTOR3* out,
IDirect3DDevice9* pDev,
int sx,
int sy,
float z,
D3DXMATRIX* view,
D3DXMATRIX* proj
) {
// ビューポート行列を作成
D3DXMATRIX vpMat;
D3DXMatrixIdentity( &vpMat );
D3DVIEWPORT9 vp;
pDev->GetViewport( &vp );
vpMat._11 = (float)vp.Width / 2;
vpMat._22 = -1.0f * (float)(vp.Height / 2);
vpMat._33 = (float)vp.MaxZ - vp.MinZ;
vpMat._41 = (float)( vp.X + vp.Width / 2 );
vpMat._42 = (float)( vp.Y + vp.Height / 2 );
vpMat._43 = vp.MinZ;
// スクリーン位置をワールドへ
out->x = (float)sx;
out->y = (float)sy;
out->z = z;
D3DXMATRIX invMat, inv_proj, inv_view;
D3DXMatrixInverse( &invMat, 0, &vpMat );
D3DXMatrixInverse( &inv_proj, 0, proj );
D3DXMatrixInverse( &inv_view, 0, view );
invMat *= inv_proj * inv_view;
return D3DXVec3TransformCoord( out, out, &invMat );
}
最初に描画デバイスに登録してあるビューポート情報からビューポート行列を作成しています。次にビューポート行列、引数のビュー行列と射影変換行列の逆行列をそれぞれ求め、ビューポート、射影変換、ビューの順番で掛け算しています。この合成行列に対してスクリーン座標を左から掛けると、ワールド空間に写像されてきます。
引数のz成分の値は0.0〜1.0の範囲を与えます。0.0を与えるとカメラの目の前にある近平面までのz成分値(ワールド空間の)、1.0にすると一番遠い所にある遠平面までのz成分値が求まる事になります。
この関数を使って近平面から遠平面まで貫くレイを作れます。すなわち、レイの開始点に当たる(sx,
sy, 0.0 ) 及び終点に当たる( sx, sy, 1.0 )というスクリーン座標を関数に渡して、ワールド空間でのレイベクトルを作ってしまえばよいわけです。
後は先に掲載しましたレイと境界球との交差判定関数を使えば、めでたく交差点に当たる球の表面を指し示す事ができるようになります!
球とスクリーンベースのレイの交差判定は、例えばFPSで標準に入っているモデルに弾が当たったかどうかなどで使えそうです。また、マウスで物をつまむ時にも活躍しそうですね。色々な場面で活躍する衝突判定です。