3D衝突編
その18 直線とAABB
直線とAABBの交差判定は概念がわかればそれほど難しくはありません。
① スラブ
2つの平行な平面で挟まれた厚みのあるプレートを「スラブ(slab)」と言います。OBBは互いに垂直な3つのスラブが交差した状態と言えます。AABBはさらに各スラブが軸に垂直になっています。
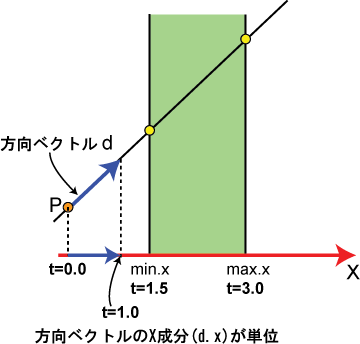
スラブは無限に広がるプレートなので、スラブに平行でない直線は必ず交差する事になります。例えばX軸に垂直なスラブと直線の関係は下図のようになります:
直線上の一点Pから双方のスラブ面までの到達間隔tは方向ベクトルd(正規化します)のX成分の大きさを単位として次のように計算ができます:
近面: t_near = ( min - p.x ) / d.x
遠面: t_far = ( max - p.x ) / d.x
この到達間隔が判定の鍵となります。
② 2DのAABB
2DのAABBは2つのスラブで囲まれた範囲です。そこに直線を引くと次の2つのパターンが考えられます:
直線PはAABBと交差しています。この時、「到達間隔にも交差」が起きているのがわかります。一方で直線QとAABBを見ると、到達間隔の交差が起こっていません。これを調べると衝突が判定できます。
具体的なプロセスです。まず、X軸垂直のスラブについて到達時刻を算出します(P.X.tmin、P.X.tmax)。次にY軸垂直のスラブの到達時刻を調べます。到達時刻のうち入り側についてはより遅い方、出側についてはより早い方の到達間隔を取ります。
直線Pについてみてみると、より遅い入り間隔はP.X.tmin、より早い出間隔はP.Y.maxです。出間隔から入り間隔を引くと(P.Y.max - P.X.min)プラスです。この場合交差が発生しています。
一方直線Qについてみると、候補入り間隔はQ.X.tmin、候補出間隔はQ.Y.maxです。同様に出-入りを算出するとマイナスです。この場合は交差していません。
③ 3DのAABB
3DのAABBの場合パターンが増えますが、プロセスは変わりません。XYZそれぞれの入り間隔及び出間隔を調べ、候補入り間隔と出間隔を決定し、引き算します。結果がプラスならば交差しています。マイナスだったら交差していません。
3DのAABBについてなんとか図を描こうと思ったのですが、どうやってもカオスになってしまいます(T_T)。すいませんが②の図を3次元にして頭で想像して下さい。
④ 直線とAABBの交差判定関数公開
最後はいつものように判定関数を公開します。ご自由にお使い下さい。
/**
* @brief 光線と境界ボックスとの交差判定
* @param pos ワールド空間での光線の基点
* @param dir_w ワールド空間での光線の方向
* @param aabb 境界ボックス(ローカル)
* @param mat 境界ボックスのワールド変換行列
* @param t 衝突間隔(出力)
* @param colPos 衝突位置
* @return 衝突していればtrue
*/
bool ColRayBox(
D3DXVECTOR3* pos,
D3DXVECTOR3* dir_w,
AABB* aabb,
D3DXMATRIX* mat,
float& t,
D3DXVECTOR3* colPos = 0 )
{
// 光線を境界ボックスの空間へ移動
D3DXMATRIX invMat;
D3DXMatrixInverse( &invMat, 0, mat );
D3DXVECTOR3 p_l, dir_l;
D3DXVec3TransformCoord( &p_l, pos, &invMat );
invMat._41 = 0.0f;
invMat._42 = 0.0f;
invMat._43 = 0.0f;
D3DXVec3TransformCoord( &dir_l, dir_w, &invMat );
// 交差判定
float p[ 3 ], d[ 3 ], min[ 3 ], max[ 3 ];
memcpy( p, &p_l, sizeof( D3DXVECTOR3 ) );
memcpy( d, &dir_l, sizeof( D3DXVECTOR3 ) );
memcpy( min, &aabb->min, sizeof( D3DXVECTOR3 ) );
memcpy( max, &aabb->max, sizeof( D3DXVECTOR3 ) );
t = -FLT_MAX;
float t_max = FLT_MAX;
for ( int i = 0; i < 3; ++i ) {
if ( abs( d[ i ] ) < FLT_EPSILON ) {
if ( p[ i ] < min[ i ] || p[ i ] > max[ i ] )
return false; // 交差していない
} else {
// スラブとの距離を算出
// t1が近スラブ、t2が遠スラブとの距離
float odd = 1.0f / d[ i ];
float t1 = ( min[ i ] - p[ i ] ) * odd;
float t2 = ( max[ i ] - p[ i ] ) * odd;
if ( t1 > t2 ) {
float tmp = t1; t1 = t2; t2 = tmp;
}
if ( t1 > t ) t = t1;
if ( t2 < t_max ) t_max = t2;
// スラブ交差チェック
if ( t >= t_max )
return false;
}
}
// 交差している
if ( colPos ) {
*colPos = *pos + t * (*dir_w);
}
return true;
}
AABBはこちらです。
struct AABB {
D3DXVECTOR3 min;
D3DXVECTOR3 max;
};
⑤ 参照
ゲームプログラミングのためのリアルタイム衝突判定 p179 5.3.3 ボックスに対する光線や線分の交差