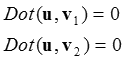
3D衝突編
その19 直線同士の最接近距離と最接近点を知る
2本の直線の最接近距離とそれを繋ぐ点の座標を求めてみます。
① 直線の定義
直線は直線上の1点Pと方向ベクトルv(標準化します)で定義するのが一般的です。今直線2本をL1、L2と表現する事にします。各記号に付く添え字の数字も属する直線を表すとしましょう。
② 最短距離を結ぶ線とはいずれも垂直関係
直線L1、L2の最短距離を結ぶ線は、双方の直線といずれも垂直な関係になります。今その垂線との交点をそれぞれQ1、Q2とし、Q1からQ2へ向かうベクトルをuとます。すると次の関係がある事がわかります:
Q1はL1上の点です。Q2はL2上の点です。よって双方は次のように表現できます:
これを上の内積の式に代入してみるとこうなります:
D1,D2,Dvは定数です。2つの式があって、未知のt、sがあるので、これは連立方程式として解く事ができます。結果としてt1及びt2は次式になります:
これをQ1及びQ2に代入すれば最短距離を結ぶ2点を算出できます。またベクトルuの長さが最短距離となります:
③ 2直線が平行の場合
上のt1及びt2の分母が0になる場合があります。Dvはdot(v1,v2)で、これが1.0fもしくは-1.0fになる場合です。これは2つの直線が平行状態の時に起こります。この場合、Q1とQ2を決める事ができませんが、最短距離はP1P2ベクトルとv1との「外積」で算出されるベクトルの長さで計算できます:
もちろんプログラム上ではDvが0である事をチェックしないと0除算エラーが発生してしまうので注意です。
③ 関数公開
いつものように2直線の最短距離と双方の直線上にある最接近点を算出する関数を公開します:
///////////////////////////////////////////////////
// 2直線の最短距離と最短点値算出関数
// pp1: 直線1上の1点
// pv1: 直線の方向ベクトル
// pp2: 直線2上の1点
// pv2: 直線2の方向ベクトル
// pOut_dist : 最短距離(出力)
// pOut_pos1 : 直線1上の最短点座標
// pOut_pos2 : 直線2上の最短点座標
bool Calc2LineNearestDistAndPos(
D3DXVECTOR3* pp1,
D3DXVECTOR3* pv1,
D3DXVECTOR3* pp2,
D3DXVECTOR3* pv2,
float* pOut_dist,
D3DXVECTOR3* pOut_pos1,
D3DXVECTOR3* pOut_pos2
) {
D3DXVECTOR3 v1, v2;
D3DXVECTOR3 &p1 = *pp1, &p2 = *pp2;
D3DXVec3Normalize( &v1, pv1 );
D3DXVec3Normalize( &v2, pv2 );
float D1 = D3DXVec3Dot( &(p2 - p1), &v1 );
float D2 = D3DXVec3Dot( &(p2 - p1), &v2 );
D3DXVECTOR3 cross ;
float Dv = D3DXVec3LengthSq( D3DXVec3Cross( &cross, &v1, &v2 ) );
if (Dv < 0.000001f) {
if ( pOut_dist ) {
D3DXVECTOR3 v;
*pOut_dist = D3DXVec3Length( D3DXVec3Cross( &v, &(p2 - p1), &v1 ) );
}
return false;
}
float Dv = D3DXVec3Dot( &v1, &v2 );
float t1 = ( D1 - D2 * Dv ) / ( 1.0f - Dv * Dv );
float t2 = ( D2 - D1 * Dv ) / ( Dv * Dv - 1.0f );
D3DXVECTOR3
Q1 = p1 + t1 * v1,
Q2 = p2 + t2 * v2;
if ( pOut_dist )
*pOut_dist = D3DXVec3Length( &(Q2 - Q1) );
if ( pOut_pos1 )
*pOut_pos1 = Q1;
if ( pOut_pos2 )
*pOut_pos2 = Q2;
return true;
}
コピペで直ぐに使えますのでご利用下さい。