3D衝突編
その1 点と線
3D空間での衝突判定の手始めとして点と線の衝突を考えてみます。考え方は2Dと同じで、線上の始点と点までのベクトルと、線の方向を示すベクトルが平行ならば点は線の上に存在します。
① 線に衝突する点
3D空間での線と点を次のように定義します。
線 : 線上の点P0(x0, y0, z0)、線の方向を示すベクトルv=(vx, vy, vz)
点 : P1(x1, y1, z1)
2Dの時と同じように、P0を始点としてP1を終点とするベクトルv1を算出し、このベクトルがvと平行ならば、点は線の上に存在します。2Dでこれを判定する時には外積を使いましたが、3Dの場合は外積は法線ベクトルになってしまいます。しかし、平行なベクトルから求めた法線ベクトルはゼロベクトルになってしまうので(詳しくはこちら)、その大きさで判定すれば良いことになります。
|v1×v|が0ならば衝突を起こしている
② 線分に衝突する点
線分は線を2点で区切った物ですから、少なくとも点が線の上にあることが条件になります。よって、まず①からそれを判定します。線に衝突していることが分かったら、次に線分の長さに対して線分の端から点までの長さを調べ、短ければ点は線分と衝突しています。
線分 : Ps(sx,sy,sz), Pe(ex,ey,ez)
点 : P1(x1, y1, z1)
線分の方向を表すベクトルをv=(ex-sx, ey-sy, ez-sz)、PsからP1へ向かうベクトルをv1としましょう。これで①と同じ作業ができます。またベクトルの大きさが、そのまま線分の長さにもなります。線分に衝突する点をまとめます。
|v1×v|が0、かつ|v1|≦|v|ならば衝突を起こしている
意外とあっさりできるもんです(^-^)
(2009. 4. 4追記)
③ 点から線分への最短ルート
点から線分までの最短ルートには2つの状態があります。1つは点から線分に垂線を下ろせる場合。この時はその垂線が最短ルートになります。もう1つは垂線を下ろすと線分の外になってしまう場合。この時は線分の両端まで引いた線で長さが短いほうが最短ルートになります。
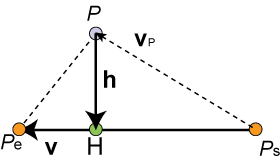
最短ルートはベクトルhを求めれば良いわけです。ベクトルhは、PからPsへ行ってPsからHへ行くルートと見ると、
h = PPs + PsH = -Vp + PsH
で、ベクトルVpは既知(P-Ps)ですから、ベクトルPsHがわかればベクトルhもわかります。
ベクトルPsHは線分上にあり、ベクトルVと同じ方向を向いています。よって、
PsH = t * V
が言えます。tはベクトルVを拡縮させる係数で、この数値を求めれば終わりです。これは次のように内積から算出できます:
t = Dot( Normalize( V ), Vp ) / Length( V )
Dotは内積を表しています。内積するのは正規化したベクトルVとVpです。内積には「正規化したベクトルNと任意ベクトルAとの内積は、AをNに投影した時の長さ(符号付き)となる」という性質があります。それをここでは利用しています。内積の結果はPsからHまでの符号付き長さなので、それを割合にするためにさらにベクトルVの長さで割っています。
という事で、ベクトルhを求める式は次のようになります:
h = PsH - Vp
= t * V - Vp
= V * Dot( Normalize( V ), Vp ) / Length( V ) - Vp
点Pから線分へ下ろした足Hが線分の外にあるか否かを判定するにはtの値を見ます。tが0未満であればベクトルPsHがVと反対側を向いているわけなので、これは点Ps側に足Hがある事になります。よって、最短ルートはベクトルPPsとなります。一方tが1より大きい場合、最短ルートはベクトルPPeとなります。