3D衝突編
その20 三角ポリゴンを囲む最小境界球
特定のオブジェクトを囲う一番半径が小さい球を求める問題を「最小境界球問題」と言います。一般には論文レベルの面倒な実装が必要になるのですが、1枚の三角ポリゴンを囲む最小境界球であれば計算で求めることができます。ただし、三角ポリゴン1枚と言えども、微妙に面倒な計算が必要になってしまいます。
① 三角形の外接円が最小境界円(球)とは限らない
三角ポリゴンをぴったりと包む円は「外接円」です:
こう見ると、外接円=最小境界円(球)のように思ってしまいますが、実は違います。例えば以下のような鈍角三角形の外接円はこうなります:
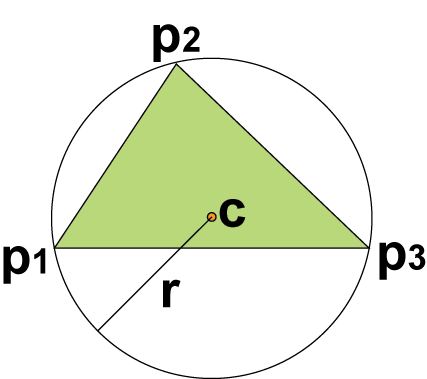
ずいぶんと大きい外接円です。この三角形を包む最も小さい境界円(球)は、辺p1p3を直径とする球です:
このように、三角ポリゴンを包む最小境界円(球)を求める時には鋭角三角形なのか鈍角三角形なのかを識別する必要があります。もし鈍角三角形ならば、最も長い辺を直径とする球が最小境界円(球)です。では、鋭角三角形の時はどうなるか?これが本章の主題です。
② 外接円は「各辺の2等分線の交点」
鋭角三角形の最小境界円(球)は、3頂点を通る球です。これは間違いなく「外接円(外接球)」です。三角形の外接円は、その三角形の各辺の2等分線の交点を中心とする円である事がわかっています:
ここから、中心点は2つの辺の2等分線の交点を求めれば良いわけです。上図の辺の中点から伸びるベクトルv1,v2,v3のどれか2つを求めれば、後は直線の交点を求める問題に帰着します。
ベクトルv1はベクトルp2p3に垂直です。また三角形に並行ですから、三角形の法線Nとは垂直関係になります。つまり、ベクトルv1はp2p3とNとの外積で求められます:
これらのベクトルがわかれば、中心点Cを通る2つの直線が次のように定義できます:
このsもしくはtが求まれば、中心点も自動的に算出できます。
さて、2Dと違い3Dの直線はめったに交差しません。数学上では交差しても浮動小数点の丸め誤差等が働くため、まともに計算すると交差しない事が殆どなんです。よって、交差問題を「2つの直線間の最小距離」となる2点を求める問題に置き換えることにします。これで実用上十分な中心点Cが算出できます。
上の式でベクトルc1c2とベクトルv1及びベクトルv2は垂直です。これは内積が0という事なので、
が成り立ちます。これを展開すると、
となり、連立一次方程式が出てきます。各内積は全部計算が出来ますので、上の式は次のように簡素に表現できます:
こういう連立一次方程式は行列を使うとさっくりと解けます。上の式は、
と逆行列を使うと解けます。上の式から、s及びtは、
と一発で求められます。ただし分母が0はまずいのでチェックが必要です。分母が0になるのは2直線が並行になる時ですが、三角形が縮退していなければこの問題は生じません。
③ 三角ポリゴン最小境界球関数
三角ポリゴン最小境界球を求める関数を公開します:
// 三角ポリゴン最小境界球
// p : 三角ポリゴンの頂点
// pos : 境界球の中心座標(戻り値)
// 戻り値: 境界球の半径
float calcBoundingSphereForTriangle(D3DXVECTOR3 p[3], D3DXVECTOR3 &pos) {
// 鈍角を探します
// 鈍角三角形の場合はその対辺の中点が球の中心で両頂点までの距離が半径。
float dot0 = D3DXVec3Dot(&(p[1] - p[0]), &(p[2] - p[0]));
if (dot0 <= 0.0f) {
pos = (p[1] + p[2]) / 2.0f;
return D3DXVec3Length(&(p[1] - p[2])) / 2.0f;
}
float dot1 = D3DXVec3Dot(&(p[0] - p[1]), &(p[2] - p[1]));
if (dot1 <= 0.0f) {
pos = (p[0] + p[2]) / 2.0f;
return D3DXVec3Length(&(p[0] - p[2])) / 2.0f;
}
float dot2 = D3DXVec3Dot(&(p[0] - p[2]), &(p[1] - p[2]));
if (dot2 <= 0.0f) {
pos = (p[0] + p[1]) / 2.0f;
return D3DXVec3Length(&(p[0] - p[1])) / 2.0f;
}
// 鋭角三角形でした
// 3頂点から等距離にある点が中心。連立方程式を解きます。
D3DXVECTOR3 N;
D3DXVec3Cross(&N, &(p[1] - p[0]), &(p[2] - p[0]));
D3DXVECTOR3 v0, v1, e0, e1;
D3DXVec3Cross(&v0, &(p[2] - p[1]), &N);
D3DXVec3Cross(&v1, &(p[2] - p[0]), &N);
e0 = (p[2] + p[1]) * 0.5f;
e1 = (p[2] + p[0]) * 0.5f;
float a = D3DXVec3Dot(&v0, &v1);
float b = D3DXVec3Dot(&v0, &v0);
float c = -D3DXVec3Dot(&(e1-e0), &v0);
float d = D3DXVec3Dot(&v1, &v1);
float e = -D3DXVec3Dot(&(e1-e0), &v1);
float div = -a*a + b*d;
float t = (-a*c + b*e) / div;
float s = (-c*d + a*e) / div;
pos = e0 + s * v0;
return D3DXVec3Length(&(pos - p[0]));
}
添字がズレているのは・・・ご愛嬌っす(^-^;;