3D衝突編
その24 レイと球の貫通点
レイを世界に向けてブシッと飛ばした時に球と衝突しているか調べるには、球の中心点からレイ(半線分)に向けて垂線を降ろし、その長さが球の半径よりも短いか否かを調べればOKです。ただ、時にレイが貫通した場所を知りたい時があります。
① 結果は内積と解の公式で出ます
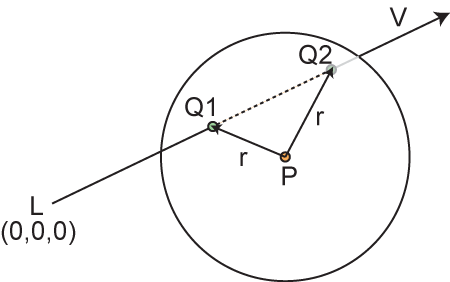
まず球の中心点をP'、半径をrとします。またレイの始点をL、レイの方向ベクトルをVとします。このままでも計算できるのですが、計算を少し簡単にするため、レイの始点Lを原点に平行移動させます。ここから球の中心点の座標はP=P'-Lと変換されます:
レイ上の1点をQとすると、Lが原点なのでQは単純に、
と表せます。aが大きくなる程レイが伸びるというイメージです。このレイが伸びて球と衝突して突き抜けた場合、その貫通点は多くの場合2点(Q1、Q2)になります(接する場合のみQ1=Q2)。球の中心点PからQ1及びQ2までの距離はいずれも半径rです。これを式で表現すると:
となります。同じベクトルの内積はベクトルの長さ(ノルム)のべき乗になりますね。またこのQ1、Q2は定義からレイ上にあります。よって、上のQにaVを代入すると、
ここで、
です。ここから、解の公式でaを算出できます:
ベクトルVの長さの係数となるaがちゃんと2つ出てきましたね。レイをベクトルVの方向に飛ばすという事は、aの値は0以上を想定します。ただ上の解ではaがマイナス値になる事もあります。aがマイナスという事は、貫通点がレイの逆方向にあるという事です。また、aの実数解が得られない事もあります。それはそもそもレイが球と衝突しないという事です。
最後に、ここまでの計算はレイの開始点を原点とした場合だったので、衝突点Q1及びQ2を次のように算出して終了です:
Q1が貫通開始点、Q2が貫通終了点となります。
② 関数公開
レイと球の貫通点の座標を求める関数を公開します:
レイと球の衝突座標を算出 // lx, ly, lz : レイの始点
// vx, vy, vz : レイの方向ベクトル
// px, py, pz : 球の中心点の座標
// r : 球の半径
// q1x, q1y, q1z: 衝突開始点(戻り値)
// q2x, q2y, q2z: 衝突終了点(戻り値)
bool calcRaySphere(
float lx, float ly, float lz,
float vx, float vy, float vz,
float px, float py, float pz,
float r,
float &q1x, float &q1y, float &q1z,
float &q2x, float &q2y, float &q2z
) {
px = px - lx;
py = py - ly;
pz = pz - lz;
float A = vx * vx + vy * vy + vz * vz;
float B = vx * px + vy * py + vz * pz;
float C = px * px + py * py + pz * pz - r * r;
if ( A == 0.0f )
return false; // レイの長さが0
float s = B * B - A * C;
if ( s < 0.0f )
return false; // 衝突していない
s = sqrtf( s );
float a1 = ( B - s ) / A;
float a2 = ( B + s ) / A;
if ( a1 < 0.0f || a2 < 0.0f )
return false; // レイの反対で衝突
q1x = lx + a1 * vx;
q1y = ly + a1 * vy;
q1z = lz + a1 * vz;
q2x = lx + a2 * vx;
q2y = ly + a2 * vy;
q2z = lz + a2 * vz;
return true;
}
球とレイとの衝突に加えて円柱とレイとの衝突が出来ると、そこから「カプセルとレイの衝突」が導けます。実はそれをやりたいがためにこの章を書きました(^-^;。という事で次は円柱(無限長円柱)とレイとの貫通点の算出です。