3D衝突編
その27 カプセルとカプセル
カプセルは「長い物」の衝突図形として非常に重宝されます。カプセル自体は「半径rな球を点AからBまでまっすぐ動かした軌跡」です。よって、カプセル同士の衝突は「2つの線分間の最短距離が双方の半径の合計よりも短いか否か」で判断できます。カプセル同士の衝突は「2線分間の最短距離問題」に帰着する訳です。
① 点から直線までの最短距離問題
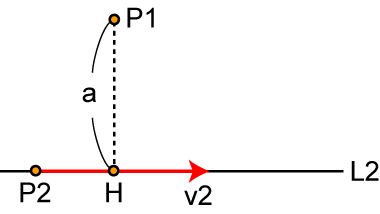
直線間の最短距離を求めるために、まずは点と直線間の最短距離を求める問題から始めます。空間内のある点をP1とします。対する直線はある点P2とその方向ベクトルv2で定められます:
この点P1と直線間の最短距離は、P1から直線まで下ろした垂線の距離になります。その足をHとしましょう。点Hの座標がわかれば最短距離もわかりますね。点Hは直線L2上にあり、またベクトルv2とベクトルP1Hは垂直です。これらを式に直すとこうなります:
係数tを調整すると点Hになります。求めたいのはtという事です。上式を下の内積のHに代入して展開すると、
このようにtは既知のベクトルを使った内積だけで簡単に求まります。tが求まれば垂線の足の座標Hも即座に求まりますし、HがわかればベクトルP1Hから距離も求まります。
点から直線までの最短距離を求めるプログラムはこの先ちらほら使われますので、ツールとして確立してしまいましょう:
// 点と直線の最短距離
// p : 点
// l : 直線
// h : 点から下ろした垂線の足(戻り値)
// t :ベクトル係数(戻り値)
// 戻り値: 最短距離
float calcPointLineDist( const Point &p, const Line &l, Point &h, float &t ) {
float lenSqV = l.v.lengthSq();
t = 0.0f;
if ( lenSqV > 0.0f )
t = l.v.dot( p - l.p ) / lenSqV;
h = l.p + t * l.v;
return ( h - p ).length();
}
上関数内で使用しているPointとかLineは3D衝突編その0「3Dプリミティブの型定義」で定義しております。直線の方向ベクトルがゼロベクトルの場合(lenSqV == 0)、直線が縮退してしまっているため基準点P2との距離を返しています。
② 点から線分までの最短距離問題
続いて点から線分までの最短距離の問題です。線分は端点がありますので直線よりも少しだけ複雑になります:
左と右の違いは、点P1が端点から伸びる垂線の内側にあるかどうかです。内側にある場合(左図)、点と直線の最短距離と同じ問題になります。一方外側にある場合(右図)、最短距離はより近い端点までの距離になります。よって、「内側か外側か」を判定できれば解決できそうです。方法は簡単で、∠P1P21P22及び∠P1P22P21の角度を調べます。鈍角があればそちら側に位置していることになります。角度が鈍角かどうかは内積を計算し、符号がマイナスかどうかで判定出来ます。これもツール化してしまいます(^-^):
// ∠p1p2p3は鋭角?
bool isSharpAngle( const Point &p1, const Point &p2, const Point &p3 ) {
return ( p1 - p2 ).isSharpAngle( p3 - p2 );
}
上関数は鋭角ならtrueなので、鈍角かを判定する場合はfalseでチェックです。これを使って最短距離を求める関数を作ります:
// 点と線分の最短距離
// p : 点
// seg : 線分
// h : 最短距離となる端点(戻り値)
// t : 端点位置( t < 0: 始点の外, 0 <= t <= 1: 線分内, t > 1: 終点の外 )
// 戻り値: 最短距離
float calcPointSegmentDist( const Point &p, const Segment &seg, Point &h, float &t ) {
const Point e = seg.getEndPoint();
// 垂線の長さ、垂線の足の座標及びtを算出
float len = calcPointLineDist( p, Line( seg.p, e - seg.p ), h, t );
if ( isSharpAngle( p, seg.p, e ) == false ) {
// 始点側の外側
h = seg.p;
return ( seg.p - p ).length();
}
else if ( isSharpAngle( p, e, seg.p ) == false ) {
// 終点側の外側
h = e;
return ( e - p ).length();
}
return len;
}
ここまでは順調(^-^)。
③ 2直線間の最短距離問題
少しずつ本番に近づいています。次は2つの直線間の最短距離です。
一方の直線をL1、他方をL2とします。直線を定めるために起点をそれぞれP11、P21、またその方向ベクトルをV1、V2とします(下図参照)。L1上の任意の点をP1、L2上の任意点をP2とします。いきなり結論ですが、直線が平行でない場合、ベクトルP1P2がL1とL2双方に垂直になる場合が最短です。なぜか?L1上の任意の点P1からは直線L2に対して必ず垂線を下す事が出来ます。①の図のような感じですね。L2側のその垂線の足をP2とすると、ベクトルP1P2とL2は垂直です。しかしこの段階でP1P2とL1とはもちろん垂直ではありません。一応その長さをaとしておきます。次に垂線の足P2からは同様にL1に対して垂線を下せます。その垂線の長さは必ず先のaより短くなりますよね。この垂線降ろしを繰り返していくと、線分P1P2とL1及びL2の角度はどんどん垂直に近づいて行きます。最終的にP1からL2に垂線を下しても、P2からL1に垂線を下しても変化が起こらなくなったらそれは最小距離に他なりません。
点P1、P2は直線の定義から次のように表せます:
P1からL2に向けて降ろした垂線の足をP2とすると、①で導いたtを求める式をそのまま使ってP2の座標を決めるt2を求められます:
今ベクトルP1P2とL1も垂直です。つまり双方の内積が0。ここからt1を求める方程式を解いていきます:
という事で、少し長い式ですがt1は既存のベクトルの色々な内積から求められます。t1が分かればt2も求まり、P1とP2も求まるので、ベクトルP1P2の長さ(=最小距離)も求まるという流れです。
○ 2直線が平行の場合
2つの直線が平行の場合、上の式の分母が0になってしまいます。つまり上の式は使えません。ただ話は簡単で、平行の場合はどの垂線も同じ長さなので、点P11と直線L2の最短距離の問題に帰着します。
2直線間の最短距離の問題もツールとして確立してしまいましょう:
// 2直線の最短距離
// l1 : L1
// l2 : L2
// p1 : L1側の垂線の足(戻り値)
// p2 : L2側の垂線の足(戻り値)
// t1 : L1側のベクトル係数(戻り値)
// t2 : L2側のベクトル係数(戻り値)
// 戻り値: 最短距離
float calcLineLineDist( const Line &l1, const Line &l2, Point &p1, Point &p2, float &t1, float &t2 ) {
// 2直線が平行?
if ( l1.v.isParallel( l2.v ) == true ) {
// 点P11と直線L2の最短距離の問題に帰着
float len = calcPointLineDist( l1.p, l2, p2, t2 );
p1 = l1.p;
t1 = 0.0f;
return len;
}
// 2直線はねじれ関係
float DV1V2 = l1.v.dot( l2.v );
float DV1V1 = l1.v.lengthSq();
float DV2V2 = l2.v.lengthSq();
Vec3 P21P11 = l1.p - l2.p;
t1 = ( DV1V2 * l2.v.dot( P21P11 ) - DV2V2 * l1.v.dot( P21P11 ) ) / ( DV1V1 * DV2V2 - DV1V2 * DV1V2 );
p1 = l1.getPoint( t1 );
t2 = l2.v.dot( p1 - l2.p ) / DV2V2;
p2 = l2.getPoint( t2 );
return ( p2 - p1 ).length();
}
お、意外と短い(^-^)。
さて、ここまでツールが揃えばカプセル同士の衝突は随分と考えやすくなります。
④ 2線分間の最短距離
さ、本丸の2線分間の最短距離のお話です。線分(Segment)は始点と終点があれば定義出来ます。線分S1を始点P11、終点P12、線分S2を始点P21、終点P22でそれぞれ定義します。2線分の最短距離を求めるに当たり幾つか場合分けを考える必要があります:
まず最初に、線分を直線と見立てて2直線の最短距離(赤いライン)を算出します。すると、大きく2つのパターンに分かれます。一つは左上図のように垂線が双方の線分の間にあるパターン。この時垂線の端点の位置を表す係数t1とt2は0と1の間に収まります。これは最短距離がうまく求まっちゃったラッキーパターンとなります。
一方S1側の端点が外に出てしまった場合が右上図です。図ではt=1.2となっています。この場合、まずt1の値を0~1の間にクランプします(上の場合はt1=1.0)。その後クランプした位置からS2に向けて垂線を降ろします。もしその足がS2内に入っていれば(例ではt2=0.7でS2上にある)それが最短距離となる線分(緑色のライン)となります。
左下図は右上図と同様にS1側が外に出てしまっています。右上図と同様にt1=1.0にクランプして、垂線を降ろします。しかし今回はその足もS2の外に出ています(t2=1.2)。この場合は今度はt2側を0~1の範囲にクランプします。そしてそのクランプ位置からS1に向けて再度垂線を降ろします。するとt1=0.7となりS1線分上に足があるのが分かりました。よってこれが最短ライン(緑色のライン)となります。
右下図は左下の図と同じような操作をした結果、最後まで垂線の足が双方の線分上に無かったパターンです。この場合、その操作によってt1とt2が最短を結ぶ端点上になっていますので、それを採用します。
○ 線分が平行な場合
2つの線分が平行になっている場合は、最初に行う2直線間の最短距離となる垂線を求める作業をスキップし、P11から降ろした垂線が最短だと仮に決めてしまいます。つまりt1=0.0としてその垂線の足を表すt2を求めます。その足がS2上に存在したら、先の左上図と同じ構造になるので決定。存在していなかったら上と同じような操作をすると最短となるP1、P2(を表すt1、t2)がおのずと出てきます。
○ 縮退している場合
S1とS2のどちらか、もしくは両方が縮退してしまっている場合があります。もしS1とS2の両方が縮退しているなら、それは始点同士の距離の問題になりますから簡単です。S1およびS2のどちらかが縮退している場合、点と線分の最短距離の問題になります(すでに導出済みです。線分が縮退しているかどうかは、線分の方向ベクトルの長さが0かどうかで判断します。
という事で、以上を考慮した2線分の最短距離を求めるツールを作成です:
// 0~1の間にクランプ
void clamp01( float &v ) {
if ( v < 0.0f )
v = 0.0f;
else if ( v > 1.0f )
v = 1.0f;
}
// 2線分の最短距離
// s1 : S1(線分1)
// s2 : S2(線分2)
// p1 : S1側の垂線の足(戻り値)
// p2 : S2側の垂線の足(戻り値)
// t1 : S1側のベクトル係数(戻り値)
// t2 : S2側のベクトル係数(戻り値)
// 戻り値: 最短距離
float calcSegmentSegmentDist( const Segment &s1, const Segment &s2, Point &p1, Point &p2, float &t1, float &t2 ) {
// S1が縮退している?
if ( s1.v.lengthSq() < _OX_EPSILON_ ) {
// S2も縮退?
if ( s2.v.lengthSq() < _OX_EPSILON_ ) {
// 点と点の距離の問題に帰着
float len = ( s2.p - s1.p ).length();
p1 = s1.p;
p2 = s2.p;
t1 = t2 = 0.0f;
return len;
}
else {
// S1の始点とS2の最短問題に帰着
float len = calcPointSegmentDist( s1.p, s2, p2, t2 );
p1 = s1.p;
t1 = 0.0f;
clamp01( t2 );
return len;
}
}
// S2が縮退している?
else if ( s2.v.lengthSq() < _OX_EPSILON_ ) {
// S2の始点とS1の最短問題に帰着
float len = calcPointSegmentDist( s2.p, s1, p1, t1 );
p2 = s2.p;
clamp01( t1 );
t2 = 0.0f;
return len;
}
/* 線分同士 */
// 2線分が平行だったら垂線の端点の一つをP1に仮決定
if ( s1.v.isParallel( s2.v ) == true ) {
t1 = 0.0f;
p1 = s1.p;
float len = calcPointSegmentDist( s1.p, s2, p2, t2 );
if ( 0.0f <= t2 && t2 <= 1.0f )
return len;
}
else {
// 線分はねじれの関係
// 2直線間の最短距離を求めて仮のt1,t2を求める
float len = calcLineLineDist( s1, s2, p1, p2, t1, t2 );
if (
0.0f <= t1 && t1 <= 1.0f &&
0.0f <= t2 && t2 <= 1.0f
) {
return len;
}
}
// 垂線の足が外にある事が判明
// S1側のt1を0~1の間にクランプして垂線を降ろす
clamp01( t1 );
p1 = s1.getPoint( t1 );
float len = calcPointSegmentDist( p1, s2, p2, t2 );
if ( 0.0f <= t2 && t2 <= 1.0f )
return len;
// S2側が外だったのでS2側をクランプ、S1に垂線を降ろす
clamp01( t2 );
p2 = s2.getPoint( t2 );
len = calcPointSegmentDist( p2, s1, p1, t1 );
if ( 0.0f <= t1 && t1 <= 1.0f )
return len;
// 双方の端点が最短と判明
clamp01( t1 );
p1 = s1.getPoint( t1 );
return ( p2 - p1 ).length();
}
しんどいコード(^-^;。
⑤ カプセル同士の衝突
すでに④でほぼ答えが出尽くしているのですが、カプセル同士の衝突は2線分の最短距離dが求めれば即座にわかります。カプセルは半径rの球がスウィープした図形なので、2つのカプセルが衝突しているというのは、2つのカプセルの球半径が最短距離dより短い時に他なりません:
// カプセル同士の衝突判定
// c1 : S1(線分1)
// c2 : S2(線分2)
// 戻り値: 衝突していたらtrue
bool colCapsuleCapsule( const Capsule &c1, const Capsule &c2 ) {
Point p1, p2;
float t1, t2;
float d = calcSegmentSegmentDist( c1.s, c2.s, p1, p2, t1, t2 );
return ( d <= c1.r + c2.r );
}
上の関数では線分同士の衝突の結果出てくる垂線の足の情報は捨てていますが、カプセルの衝突位置を粗く出力したい時などには活用できます。