3D衝突編
その2 線と線
3Dの空間にある線と線の衝突は、難しそうに感じますが、意外と簡単なんです。「平面にある平行でない線は必ず交わる」というのがポイントです。
① 線と線の衝突
2つの線が衝突するためには、少なくとも2辺が同じ平面に乗っている必要があります。これは、2つの線のベクトルの外積をとって法線ベクトルを調べれば簡単に分かります。

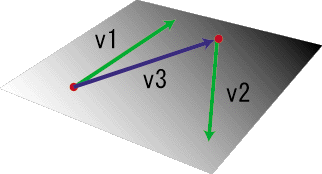
v1とv2はそれぞれ線の方向を表すベクトルです。v3は直線1上の点から直線2上の点へ伸ばしたベクトルです。これは、直線が定義されているなら必ずある点です。
v1とv2の外積を取るとそれらベクトルを含む平面の法線ベクトルn1が一意に求まります。一方v1とv3でも同様に法線ベクトルn2を求めることができます。v1とv2が上図のように同じ平面上に乗っかっているならば、当然v3も同一平面上にありますよね。よって、それらから求まる法線ベクトルn1とn2は平行になります。実はこれが衝突判定となります。
n1がゼロベクトルになる事があります。これはv1とv2が平行な時に起こります。よってn1がゼロベクトルの時には直線が交わることはありません。一方n2がゼロベクトルの場合もあります。これは唯一v3がゼロベクトル、つまり2直線上同じ点を結んだ場合に起こります。これはすでに衝突している状態ですよね。
以上から線と線の衝突判定をまとめます。
・ |n2|==0ならば衝突を起こしている。
・ |n2|!=0で、|n1|>0の時、|n1×n2|==0なら衝突を起こしている。
先に法線ベクトルの大きさを求めておけば、非常に簡単な条件分岐で衝突判定ができますね。