3D衝突編
その3 線分と平面
線分と平面の衝突は、いろいろな場面で登場します。キャラクタと地面の関係は、キャラクタを1本の線分として地面と衝突しているか判定した方が簡単です。飛んでいった弓矢が平面に刺さったかどうか、打った弾が平面に当たったかなど、応用範囲は広いと思われます。
① 線と平面の衝突
手始めに線と平面が衝突するかを考えます。これは、非常に簡単!無限に広がる平面に対して線が交わらない場合はただ1つ「平面と線(平面に含まれていない)が平行」な時だけです。これは、平面の法線ベクトルと線のベクトルが垂直関係にあればOKです。つまり、内積が0ということですね。線と平面を、
線 : 線上の点P1(x1, y1, z1), 方向を表すベクトルv=(vx,vy,vz)
平面 : 平面上の点P0(x0, y0, z0), 法線ベクトルn=(nx, ny, nz)
と定義しておきます。まず、線が平面に含まれているかを判定します。これは、点P0と点P1を結ぶベクトルv1と法線ベクトルnが垂直関係になっていれば良いわけですね。これで線が平面に含まれていないと判定された場合は、線のベクトルvと平面の法線ベクトルnの垂直関係を調べます。垂直なら衝突していません。よって、
・ v1・n == 0 もしくは、v・n != 0なら衝突を起こしている
となります。
② 線分と平面の衝突
さて、今度は線分です。線分の場合、平面と平行でなくても衝突を起こさない場合が出てきます。面倒な感じもしますが、これも意外と簡単なんです。線分は2点を結んだ部分線ですから、平面と衝突しているならば、点の一方は平面の表側、一方は裏側にあるはずです。つまり、この表裏関係を調べれば良いのです。
線分 : P1(x1,y1,z1)、P2(x2,y2,z2)
平面 : 平面上の点P0(x0, y0, z0), 法線ベクトルn=(nx, ny, nz)
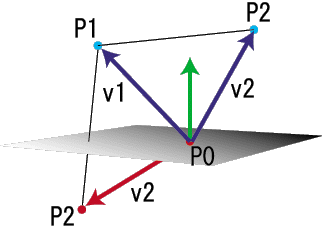
としておきます。まずは下の図をご覧下さい。

緑のベクトルが平面の法線ベクトルnです。青い点は平面と衝突していない線分の端になります。注目するのは法線ベクトルnとv1,v2の角度です。青い点が面の表側のどこにあっても、この角度は鋭角になります。色々イメージしてみてください。必ず90度以下になります。一方P2が平面の下側にある場合(赤い点)、法線ベクトルnとの角度は鈍角になります。ということは、法線ベクトルnとv1,v2の内積をとって、その符号が異なると線分は平面と衝突していることになります。
線分と平面の衝突をまとめましょう。
(v1・n) * (v2・n) <= 0ならば線分は平面と衝突を起こしている
どうでしょう。とても簡単ですよね。この考え方が「ポリゴンと線分の衝突」のベースとなります。