3D衝突編その６　筒と筒

3D衝突編
その６　筒と筒

　筒と筒の衝突はそれなりな使い勝手があります。細長い構造が多い人や動物、生物などはこれによって衝突判定を行わせると良いかもしれませんが、ただ、有限の長さがある筒を扱うのはかなりに面倒だったりします。

① 筒とはボリュームのある線だ！

　筒はボリュームのある線と考えるとわかりやすくなります。

筒：基準線の方向を示すベクトルv=(vx,vy,vz), 基準線上の一点P0(x0,y0,z0), 筒の半径r

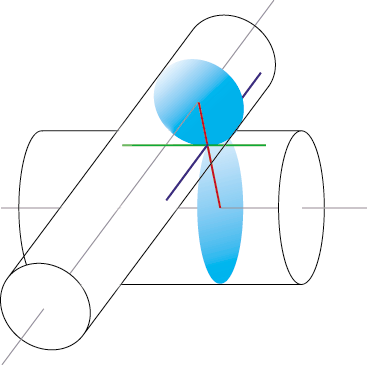
↑奇跡的にうまく描けたなぁ(^-^;

　2本の筒の接する部分にのみ注目すると、これは単に2つの円が接しているだけに過ぎません。図で言えば青い円がそれにあたります。しかも嬉しいことに、これら円は赤い線で示しているように、まっすぐな赤い軸にぴったりとくっつきます。赤い軸が円に含まれているわけです。そして、円の法線は筒内部を走る線です。ということは、赤い線と筒内部の線は常に直行する関係にあることが分かります。結局のところ、筒が衝突しているとは、2つの基準線の最短距離が筒の半径の和より短い場合を言います。

　2直線の最短距離は、基礎の基礎編その２内の「2直線の最短距離」で示している通り、割と簡単に出せます。これを使えば、筒同士の衝突も簡単です(^-^)

② 切れている筒はどうする？

　上図のような切れている筒には切り口があります。①は単に2直線間の最短距離で判定するだけでして、これは永遠に長い筒を想定しています。しかし、ゲームで使うとなると、やはり切れている筒の方が使用頻度が高いでしょう。ところが、まともに切れている筒の衝突判定をすると、基準線間の最短距離だけで判断できなくなり、衝突判定の難易度が急上昇してしまいます。具体的には「線分間の最短距離」「側面に接している場合の例外処理」が必要になります。双方とも難しいものです。

　これについては、本気で必要になった時に考えてみることにしまして、今は触れないでおきます。