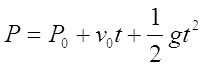
基礎の基礎編
その4 フレーム間移動は等速直線運動で
ゲームに「点の動き」は欠かす事ができません。キャラクタも、STGの弾も、パーティクルも基本的には点(制御点)の動きの集大成です。
点が物理法則に基づいて動くとゲームにリアリティーが生まれます。花火のパーティクル、舞い上がるほこりなど、ちょっとした物理現象が再現できるだけでゲームの厚みがぐっと増してきます。点の動かし方は様々ですが、物理現象と聞いてまず思いつくのが「落下運動」かなと思います。自由落下の式はこういうのでした:
P0は初期位置、v0は初速(初期位置での速度)、tは初期位置からの経過時刻、そしてそしてgはいわゆる「重力加速度」です。この式は「初期位置からtだけ経過した時の位置P」を算出してくれます。
この式は物理現象の相当に広い範囲をカバーしてくれる超大切な式なのですが、実はこの通りにゲームで使うと面倒が起こります。ゲームはフレーム単位で動く、そしてゲームの衝突は大抵の場合等速直線運動をしている物同士を考える。この2つの制約と上の式は、微妙にすれ違いがあるんです。
フレーム単位で動くゲームで物理現象を扱うにはどうしたら良いのか?この章ではその辺りの基本的な部分を試行錯誤したいと思います。
① フレーム間は等速直線運動で
ゲームは1フレーム単位で動きます。フレームの間の移動は「等速直線運動」を仮定します。これは衝突判定等の計算が非常に楽になるためです。逆にフレーム間の位置を厳密な計算にしてしまうと、非線形で時間に比例しない動きをするもの同士の衝突判定の計算が必要になります。相当に面倒なのは必至です。
一番身近な自由落下運動もその枠組みで考えます。具体的にどうするか?次の節で考えてみます。
② 自由落下をどう扱うか?
フレーム間等速直線運動をさせる時に、例えば自由落下はどう扱えば良いのでしょうか。良く知っている式は冒頭に挙げたこれです:
P0は初期位置、v0は初速、そしてgは重力加速度(-9.8m/s^2)です。しかしこの式、よく見ると時間tに対する「2次式」になっています。先ほどと重複しますが、ゲームの1フレームは等速直線運動をしないと面倒くさいことになります。例えば、この式に位置と速度と加速度を与えて次の位置を求めてしまうと、めり込みが起こった時に非線形に位置を戻す必要がでてきてしまいます:
図を見ても厄介さが色々と分かると思います。落下した球は加速し続けるので、その位置は等タイミングの時刻経過に比例しません。床に当たった瞬間の時刻を求めるにはちょっと計算が複雑になります。位置も曲線を描くため、球も床も動くような状況になると非常に面倒な計算で衝突位置と時刻を求めなければならなくなります。
諸悪(?)の根源はフレーム中に与えた加速度によって速度が加速されてしまう事にあります。そこで、上の図を次のように捉えなおしてしまいます:
フレーム間では物が等速直線運動をして次の位置に達するんだと考えるんです。こうすると衝突した時の位置や時刻を算出するのがとても簡単になります。もちろんこうすると微妙な紛れが出てきます。理屈と計算結果が一致しません。でもゲームは「らしく見えれば良し」なんです。上のようにフレーム間を等速直線運動させるのも、時間間隔が短ければ十分に落下したように見えます。
フレームの最初に設定した位置、速度そして加速度を用いると、何事も無かった場合の次の位置が算出できます。大胆にも「位置の情報はこれで近似」します。衝突時刻もこの位置情報から上の図のように逆算します。ここで大切なのは「途中の速度」です。この速度は、フレームの最初に与えた初速と加速度から計算します。これは実際は奇妙なんです。等速直線運動をしているのだけども速度は増加している!!あべこべです。でも、そうしないと衝突した時の力の計算や次のフレームの初速など、様々な部分に弊害が出てきます。
「次の位置までの位置と時刻の情報は線形補間で、間の速度は理屈通り」。これで自由落下運動をテストしてみましょう。
③ 自由落下で肩慣らし
早速自由落下(投下速度運動)をするゲームプログラムを作ってみましょう。
②でお話したような位置と速度の情報を持ってその位置を計算してくれるPhysicBaseクラスを作ります。設定メソッドは位置、速度そして加速度です。取得メソッドには基本的に2つの時間情報が必要となります。1つは「単位時間」です。ゲームであれば1/60sec。これが無いと「次の行き先」が定まりません。もう1つは「補間時間」です。単位時間の間のどの時刻の情報が欲しいのか、それを示す時刻です。これは0〜1に標準化しても良いのですが、実差分時間(1/120sec.など)を与えた方が利便性が高いのでそういう仕様にします。与えられた情報から差分時間での位置を算出するgetPosメソッド、その時の速度を取得するgetVelocityメソッドなどを作ります。
もう1つ設けたいのが内部の変数の状態を一新するupdateメソッドです。先の取得メソッドは値を取得しますが内部の状況は変えません。一方updateメソッドを呼ぶと、その時点の位置、速度に内部の変数を更新します。加速度は扱いがやっかいですが、何も指定されていなければ「0」にしてしまいます。これは、毎回加速度を外部が設定する事を意味します。加速というのは外部的な要因ですから、これは自然な方向だと思います。
クラスの宣言はこんな感じです:
PhysicBaseクラス宣言部 //! 物理的に位置を動かすクラス
class PhysicBase {
public:
PhysicBase( float unitTime = 1 / 60.f );
‾PhysicBase();
//! 更新
virtual void update( float dt, bool isResetAccel = true );
//! 位置を設定
virtual void setPos( D3DXVECTOR3 &pos );
//! 速度を設定
virtual void setVelocity( D3DXVECTOR3 &vel );
//! 加速度を設定
virtual void setAccel( D3DXVECTOR3 &acc );
//! 位置を加算
D3DXVECTOR3& addPos( D3DXVECTOR3& out, D3DXVECTOR3 &pos );
//! 速度を加算
D3DXVECTOR3& addVelocity( D3DXVECTOR3& out, D3DXVECTOR3 &vel );
//! 加速度を加算
D3DXVECTOR3& addAccel( D3DXVECTOR3& out, D3DXVECTOR3 &acc );
//! 指定時刻での位置を取得
virtual D3DXVECTOR3& getPos( D3DXVECTOR3& out, float dt );
//! 指定時刻での速度を取得
virtual D3DXVECTOR3& getVelocity( D3DXVECTOR3& out, float dt );
//! 現在の位置を取得
D3DXVECTOR3& getCurPos();
//! 現在の速度を取得
D3DXVECTOR3& getCurVelocity();
//! 現在設定されている加速度を取得
D3DXVECTOR3& getCurAccel();
protected:
float t_; //!< 差分時間
D3DXVECTOR3 pos_; //!< 位置
D3DXVECTOR3 vel_; //!< 速度
D3DXVECTOR3 acc_; //!< 加速度
};
このクラスの完全実装はこちらからダウンロードできます。ほとんどがセッターとゲッターです。ポイントになるのはgetPos、getVelocityそしてupdateメソッドです。
getPosメソッドは引数の差分時間における位置を取得します:
getPosメソッド //! 指定時刻での位置を取得
D3DXVECTOR3& PhysicBase::getPos( D3DXVECTOR3& out, float dt ) {
D3DXVECTOR3 next = vel_ * t_ + 0.5f * acc_ * t_ * t_;
out = pos_ + dt / t_ * next;
return out;
}
太文字で示した部分はいわゆる等加速度運動の式です。ここで与えているt_は単位時間です(1/60sec.)。一度この計算で次の単位時間での差分位置(差分ベクトル)を計算してしまいます。その次に引数の差分時間dt分だけ進んだ位置を算出しています。dt / t_が比率になっているのに注意して下さい。
getVelocityメソッドも実装は似たような感じです:
getVelocityメソッド //! 指定時刻での速度を取得
D3DXVECTOR3& PhysicBase::getVelocity( D3DXVECTOR3& out, float dt ) {
D3DXVECTOR3 next = acc_ * t_;
out = vel_ + dt / t_ * next;
return out;
}
速度の変化は加速度が握っています。加速度は単位時間だけ速度を増加(減少)させますので、太文字のように線形式になります。これも_tだけ加速した分を先に算出しておいて、dtとの比率で引数の時間での速度を出力しています。速度はベクトルとして取得します。スカラーではありませんのでこれも注意です。
updateメソッドは設定されている位置、速度そして加速度を元にして実際に時刻を進めます:
updateメソッド //! 位置や速度を更新
void PhysicBase::update( float dt, bool isResetAccel ) {
// 位置を算出
getPos( pos_, dt );
// 加速度から速度を算出
vel_ += acc_ * dt;
// 加速度をリセット
if ( isResetAccel )
acc_.x = acc_.y = acc_.z = 0.0f;
}
まずは位置を更新します。これは引数のdt分だけ線形で動かします(フレーム間は直線運動なので)。次に加速度から速度を更新しています。ポイントは加速度のリセットで、isResetAccelが真ならば加速度をリセットします。クラスの宣言でこの第2引数はtrueをデフォルトとしています。
このクラスを用いると、自由落下は次のような簡単なプログラムで実現できます:
自由落下のテストプログラム int _tmain(int argc, _TCHAR* argv[])
{
PhysicBase pb;
D3DXVECTOR3 g( 0, -9.8f, 0 ); // 重力加速度 (m/s^2)
float unitTime = 1 / 60.f; // 単位時間 (sec)
for ( int i = 1; i < 61; i++ ) {
pb.setAccel( g ); // 重力加速度を設定
pb.update( unitTime ); // 単位時間だけ進める
// 位置を取得
D3DXVECTOR3 pos = pb.getCurPos();
printf( "[ %f ] %f, %f, %f¥n", i / 60.f, pos.x, pos.y, pos.z );
}
return 0;
}
1秒先まで落下位置を1フレームごとに出力するプログラムです。実際に試してみると1秒後の位置のY成分は-4.900002(m)とまず問題ない状態です(理論的には-4.9m)。投てきや風の影響なども、初速ベクトルをsetVelocityメソッドで設定すれば計算できます:
上の2つは両方とも同じ初速ベクトルを持っているのですが、青い方は重力加速度に-X軸方向の加速度を加えています。これにより、風の影響っぽい様子を再現できます。
こういう基礎クラスは色々なところで必要になります。必ずしもこの形態にする必要はありませんが、何らかのクラスは作っておいた方が良いかなと思います。