基礎の基礎編
その5 反射ベクトルと壁ずりベクトル
ゲームで良くあるのが壁ずりです。その名の通り壁に当たった時にキャラクタが壁面に沿ってずりずりと動く様を言います。物理的に正しくは無いのですが、プレイヤーに極自然に「端・障害物」を感じさせることができます。
① 壁ずりベクトルの求め方
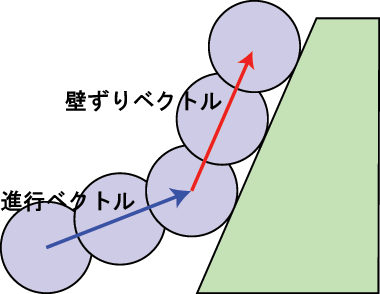
壁ずりでポイントなのは壁ずりする方向(壁ずりベクトル)です。壁に当たった時に強制的に移動させられる方向です:
上の赤いベクトルで表した壁ずりベクトルは壁に対して平行になっています。このベクトルを算出するには「当たった場所の法線」が必要です。
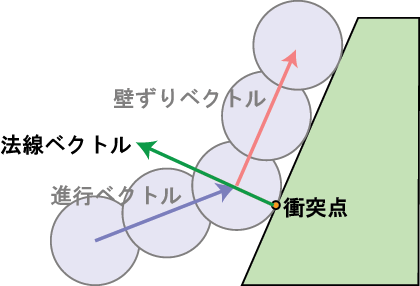
平らな壁の場合、法線ベクトルは多分既知でしょう。壁でなくとも衝突図形であれば、大体衝突点さえわかればその点での法線は求められます。
衝突点での法線ベクトル、壁への進行ベクトルがあれば壁ずりベクトルを計算できます。以下の図を御覧ください:
求めたい壁ずりベクトルを進行ベクトルの根元にもって来て、法線を進行ベクトルの先にずらしました。法線ベクトルを図内のaの長さに縮めると、壁ずりベクトルは次の式で求められます:
法線を正規化する事を忘れずにです。係数aは進行ベクトルの逆ベクトルを法線に投影した時の長さです。これは内積の基本性質になっています。つまり、
で算出できます。以上から壁ずりベクトルは、
となります。正規化した法線ベクトルと進行ベクトルだけから求められるので楽々ですね~。
② 反射ベクトルの求め方
反射ベクトルとは進行ベクトル方向に進んだ物が壁に当たって跳ね返った時の方向です。ビリヤードなどでおなじみですね:
これは次のような反射の性質から簡単に求まります:
aは①の壁ずりベクトルで出てきた係数aと全く一緒です。図からわかるように、反射ベクトルrは、
で求まります。この式、壁ずりベクトルとそっくりなんです。違うのは正規化した法線にaを掛けるか2aを掛けるかの違いだけです。上式のaに①で示したaの式を代入すると、
となります。
③ 関数公開
最後はいつものように壁ずりベクトルと反射ベクトルを求める関数を公開します:
壁ずりベクトルと反射ベクトル関数 //////////////////////////////////
// 壁ずりベクトル
//
// out : 正規化壁ずりベクトル(戻り値)
// front : 進行ベクトル
// normal: 衝突点での法線ベクトル
//
D3DXVECTOR3* calcWallScratchVector(D3DXVECTOR3* out, const D3DXVECTOR3& front, const D3DXVECTOR3& normal) {
D3DXVECTOR3 normal_n;
D3DXVec3Normalize(&normal_n, &normal);
return D3DXVec3Normalize(out, &(front - D3DXVec3Dot(&front, &normal_n) * normal_n));
}
//////////////////////////////////
// 反射ベクトル
//
// out : 正規化反射ベクトル(戻り値)
// front : 進行ベクトル
// normal: 衝突点での法線ベクトル
//
D3DXVECTOR3* calcReflectVector(D3DXVECTOR3* out, const D3DXVECTOR3& front, const D3DXVECTOR3& normal) {
D3DXVECTOR3 normal_n;
D3DXVec3Normalize(&normal_n, &normal);
return D3DXVec3Normalize(out, &(front - 2.0f * D3DXVec3Dot(&front, &normal_n) * normal_n));
}