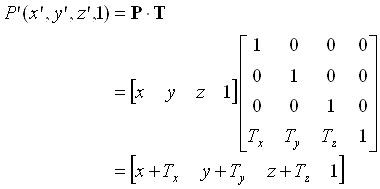
ホーム < ゲームつくろー! < DirectX技術編 < 知っていると便利?ワールド変換行列から情報を抜き出そう
その39 知っていると便利?ワールド変換行列から情報を抜き出そう
今回はちょっと息抜きです。ワールド変換行列(座標変換行列)は3Dゲームで多分一番よく使う行列だと思います。この行列は回転、スケール、オフセットの3要素から作成します。では、すでに作成されたワールド変換行列からそれらの要素は抜き出す事ができるのでしょうか?またワールド変換行列には具体的にどのような情報が詰め込まれているのでしょうか?この章では、そのようなワールド変換行列から抜き出す事ができる情報について整理してみます。
① ワールド変換行列の作り方
今更なのですが、ワールド変換行列の基本についてまとめておきます。ワールド変換行列は回転、スケール、オフセットの3要素を表す行列の掛け算で作成するのが一般的です。各行列を回転行列、スケール行列及びオフセット行列と呼ぶことにします。まずは各行列の性質について簡単に説明します。
オフセット行列は、ローカル座標空間の任意の点をワールド空間内で「平行移動」させます。
Tがオフセット行列です。点に対して右側から掛け算すると、結果の通り元の点(x,y,z)が(Tx,Ty,Yz)分だけ並行移動します。P(x,y,z)をローカル座標の位置だとすると、これはローカル座標内の点を全部平行移動する行列とも言えます。
スケール行列は、ローカル座標の任意の点を「原点を中心」として引き伸ばしたり縮めたりします。
Sがスケール行列です。結果を見ると、ローカル座標の任意の点が定数倍されています。ローカル座標空間がXYZ軸方向に独立に引き伸ばされるわけです。一般に、この行列はデフォルトのオブジェクトの大きさを変化させるのに使用します。
最後の回転行列は、3要素の中で一番メンドクサイ行列です。「ローカル座標にある点を1つの軸を中心軸として回転させる」という作用があります。どの軸で回転させるかによって行列の形が異なります。そして、これがメンドクサイ理由なんです。例えば、X軸回転の行列は次のようになります:
回転角度θは省略してあります。Y軸回転の行列は下のようになります:
Z軸は次の通り:
これらの回転行列は「原点から軸の方向を見たときに反時計回りが正」となります。回転行列は、回転順序を間違うと思った所に点を移動させられないので注意が必要です。例えばX軸上にある点について、X軸回転で90度しても(どれだけ回転しても)元の位置です。回転後それをY軸回転で90度回転すると、必ずZ軸上に移動します。一方同じ点について、先にY軸回転で90度回転させるとZ軸に移動しますが、その後X軸回転で90度すると、これはY軸上に移動することになります。同じ回転角度を与えても、軸回転の順序によって変換後の点の位置は異なってしまうわけです。よって、「ゲーム製作で回転順序を固定させる」というのが必須になるんです。ちなみに、2軸の回転があれば、点までの距離を半径とする球面上のどの点にでも移動できます。逆に言えば3軸あるからといって必ずしも3回回転をさせなければならないという物でもないわけです。
各行列は掛け算する事で連続的な変換になります。この時の掛け算の順序によって変換順番が異なります。もちろんその順番はゲーム製作の決まり事として決めるべきなのですが、使いやすさからすると「スケール変換」「回転」「オフセット」の順番かなと思います。この順番で掛け算した時のワールド変換行列は次のようになります。
R**というのは回転行列の合成によってできる数値です。回転行列は2軸であれ3軸であれ、どのように組み合わせても上の緑色の部分にしか関与しません。またスケールも緑色部分にだけ関与し、1行目にX軸、2行目にY軸そして3行目にZ軸スケールが掛け算されます(横方向に掛け算されていますね)。オフセット部分はスケールや回転と独立していて4行目の1〜3列目にXYZ軸順に位置します。
このことから、実はワールド変換行列を作成する時に、少なくともオフセット行列を掛け算する必要はありません。スケール行列と回転行列を合成した後、上の赤い部分にダイレクトにオフセット位置を書き込めばいいんです。行列を1回掛け算するコストを考えると、構造体の変数を3回書き直した方がはるかにはるかに高速です(実際デバッグで逆アセンブルしてみたのですが、D3DXMATRIX構造体が持つ演算子による掛け算はループを含め300命令以上かかっていましたが、代入だとたったの6命令です!Release時にはもっと高速な仕組みが入るのかもしれませんが、6命令以下という事は無いでしょう)。
さてこの上の関係を踏まえて、逆にワールド変換行列から何を抽出できるのかを考えてみます。
② ワールド変換行列から色々と
ワールド変換行列(座標変換行列)がぽんと出されたとして、そこから得られる事を見ていきます。便宜上行列の各要素の表し方をD3DXMATRIXのそれに統一します。ワールド変換行列はWという変数名として、例えば1行目の2列目はW._12、3行目4列目はW._34と表記します。
○ オフセット値
上の行列の色分けを見れば一目瞭然ですが、オフセット値は4行目の1,2,3列目に集約されています。つまり、
です。これは何の問題もありません。
○ スケール値
各スケールの値は緑色の部分で回転値と組み込まれてしまっています。これを取り出すのは連立方程式でも解かなければならないような気がしますよね。ところが、これは意外と簡単なんです。ワールド変換行列に対して例えば(1,0,0,0)という単位ベクトルを掛け算してみます:
すると、右辺にワールド変換行列の上の部分が抽出されてきます。左の点の4要素目は「0」になっていますね。これは「オフセットを無視しなさい!」という意味なんです(掛け算するとオフセット部分×0になるので)。つまり、右辺に出てきた点は、元の点をスケール変換して回転させた点を表す事になります。さて、左辺をベクトルだとしますとその長さは1です。これをワールド変換した右辺のベクトルは「Sxだけオフセットしてから回転」されているわけです。ベクトル(矢印)をどれだけ回転させても長さは一緒ですよね。元の長さが1なのですから、右辺のベクトルの長さというのはその物ずばり「オフセット値Sx」になります。右辺は元のワールド変換行列の1行目ずばりですから、結局のところ各スケール値というのは、
と計算されます。これはべき乗計算が入るので多少コストがかかり精度誤差も多少出ますが、スケールはワールド変換行列からちゃんと抽出できるんです。
○ 回転
実は回転については、簡単に抽出する術がありません。というのも、回転は1軸、2軸もしくは3軸回転の合成になっているからです。回転前の点を回転後の点の位置に移動させる軸回転の組み合わせは少なくとも6通りあります(XY,YZ,ZX,XYZ,YZX,ZXY)。必ず固定した2軸を使っていると決めた場合は、連立方程式によって回転角度を求める事が一応可能ですが、ジンバルロック等の関係もあって一般に計算は非常に面倒でハイコストです。どうしても各軸ごとの回転角度が必要ということならば話しは別ですが、そうでなければ潔くあきらめて、「回転行列」として扱った方が楽です。オフセット値とスケール値は算出できますので、ワールド変換行列を回転行列だけにしてしまう事はとても簡単です。
○ ローカル座標のXYZ軸がどちらに向いているか
この章で一番言いたかったのは実はここなんです(笑)。使い道が広そうな割りに案外見落とされている事かなとも思います。ワールド変換行列というのは、ローカル空間ごと変換する行列です。ということは、ローカル座標のXYZ軸もワールド空間でどちらかの方向を向いている事になります。もちろん各軸の直行関係、左手系(右手系)の関係などは変換しても変わりません。実はワールド変換行列には、その変換後の向きベクトルがしっかりと刻印されています。
先ほどスケール値の抽出で出てきた計算式をもう一度ご覧下さい。
この左辺、じ〜っとみると、これは「X軸の向き」に他なりません。ということは、右辺は変換後のX軸の向きなんです。なんと簡単な事に、各軸の変換後の向きは、ワールド変換行列の各行にそのまま刻印されているんです。まとめますと、
となります。これ、知っているのと知らないのとで大違いです。知らなかった方は是非今のうちに覚えてしまって下さい。
他にも抽出できる事があるかもしれませんが、ここで紹介した値だけでも十分に利用できます。特にローカル軸が変換後にどう向いているかというは、姿勢の制御において重要となってきます。また①の色分けしたワールド変換を見ると「位置、スケール、回転行列」と言う形でキャラクタを表しておくと便利だということも分かると思います。①の最後の方で述べましたが、行列の掛け算と言うのはMMXテクノロジを使ったとしてもコストのかかる仕事です。ですから生真面目に「スケール行列、回転行列、オフセット行列」を保持して3回も掛け算するのは馬鹿げています。もちろんそれぞれを別に保持していたとしても、ワールド変換行列を作る時にいったんこれらの行列を生成してから掛け算しては本末転倒です。ワールド変換行列の各要素は①の最後に示しましたように非常に単純な形になっていますから、各値を直接打ち込んだ方がきっと速いはずです。値の直接代入が7つ(オフセット値と0と1)、掛け算して代入が9つ(①の緑の部分)ですから、昨今のCPUならば10000回やっても一瞬でしょう。一方の行列掛け算3回×10000というのはCPUの種類にもよりますが計算時間を感じられる程度の遅さになります。ちなみに、最近のGPUであれば行列演算処理が飛びぬけていますので、この関係は同等程度か逆転します。1命令で4×4の行列の掛け算が出来る命令セットは普通にあるんです。
回転行列の生成はD3DXMatrixRotation関数関連でも良いですし、クォータニオンからD3DXMatrixRotationQuaternion関数で作成しても良いと思います。私は個人的に直感的でジンバルロックの無いクォータニオンが大好でして、後者の関数を良く利用しています。
情報がぎゅっと詰まったワールド変換行列。その性質をうまく利用したいものです。