○×的数学のお部屋
その4 斜辺10cm、高さ6cmの「ありえない」直角三角形の面積を真面目に求める
突然ですが、問題です:
斜辺が10cm、斜辺の対角までの距離(高さ)が6cmの直角三角形の面積はいくつになるでしょうか?
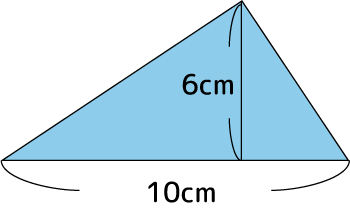
この問題、底辺が10cmで高さが6cmですから「10×6×1/2 = 30cm2!」と答えるのが普通です。しかし、実はこの直角三角形は作れません。なぜ作れないか、以下の図をご覧下さい:
直径10cmの円があります。円の直径と円周上の1点で出来る三角形は直角三角形になります。逆に言えば円周以外の点では直角三角形にはなりません。円周上の一点のうち高さが一番高くなる直角三角形は、上図から明らかなように垂線が中心を通るケースで、その時の高さは半径なので5cmです。この事から、冒頭の青い三角形のように斜辺が10cmで高さが6cmになる直角三角形は存在しないんです。よって、上の問題の答えは「そんな直角三角形は無いので面積は求められない」となります。ひっかけ問題でした~というオチです(^-^;
この問題、YouTubeを眺めていた時にたまたま出てきまして「あ~ひっかけだよねぇ」なんて思ったのですが、ふと「ちょっと待て、平面ならば分かるけどそれ以外の世界だったら設問のような直角三角形は有りうるのでは…?」と考えが及びました。設問も「平面上での~」みたいな断りは特に無かったので、空間は自由に定義出来ます。
そこで、この章では上のような「ありえない」直角三角形を定義可能な世界を定義し、その面積を求めてみたいと思います。
① 球面三角形
上の直角三角形は平面的な座標系でのお話です。しかし世の中平面座標だけとは限りません。例えば球面上にも三角形を描く事は可能です。ただしその為には「球面上での直線」をまずは定義する必要があります。
球面上での直線とは「球面上に重ならない2点A,Bを穿った時、球の中心Oとその2点を通る平面が切った球面の断面円の円周」です:
なぜこれが直線かと言うと、上図の線分ABがこの球面上でAからBへ行く最短ルートになっているからです。「直線って曲がっちゃダメなんじゃないの?」と思うかもしれませんが、それは私達が普段認識している「直交座標系」で見ているからで、球面の世界ではこれが「真っすぐ」なんです。
直線が定義できれば、直線で囲まれた多角形も定義出来ます。三角形であれば頂点が3つあれば良いので、
このように球面上の三角形(球面三角形)を作る事が出来ます。
② 斜辺10cm、高さ6cmの「球面直角三角形」
球面三角形のある頂点の角度は、その頂点を通る2つの断面円(平面)が成す角度です。例えば上の角Aの角度は平面OABとOACが作る角度となります。球面上に直角三角形(球面直角三角形)を作るには内角の一つを90度にすれば良く、それはその点を通る2断面円が直行してれば成立します:
上の角Cを成す2つの平面は直行しているので、各Cは直角です。残り2つの点を点Cを通る2直線上にそれぞれ設ければ球面直角三角形の完成です。
球が何らかの半径rを取れるとして、AとBを上手く設定すればその間の距離(円弧の長さ)を10cmにする事が出来るはずです。今それが仮に出来ているとした場合、果たして高さ(円弧ABから点Cに向かう垂線)を6cmにする事が出来るのでしょうか?
ここで話を簡単にするため作る直角三角形に制約を設けます。常にAC=BCだとしてしまいましょう。斜辺以外の2辺の長さが等しい「球面直角二等辺三角形」に限定してしまいます。そうすると、点Cから線分ABへの垂線の足Dは、常にABの中点となります:
ここで軸の登場です。中心点Oから直角である点Cを貫く方向をY軸、平面OBCに平行で点B側の方に向くのをX軸、同様に平面OACに平行でA側の方を向く軸をZ軸とします。こうすると、点AはYZ平面に、点BはXY平面に含まれることになります。またACとBCの長さは等しいので∠COA=∠COBです:
この角度をθ、球の半径をrとすると、点A、B及びCはそれぞれ、
となります。
孤ABの長さはOAとOBの成す角度をβとすると、
です。今これが10cmと仮定しているので、半径rは、
そして角度βは内積の性質から、
このように算出出来ます。
例えばθの角度が小さくなると点Aと点Bは直角の点C側に寄って行きます。その分AB間の距離は相対的に小さくなるので、逆に球の半径rを大きくしなければAB間が10cmであるという制約を保てません。rとβ、βとθの関係式はちゃんとそれを物語っています。
では次に高さであるCDの長さを求める式を考えてみましょう。今|OA|=|OB|=r、点DはABの中点、そしてOABDはすべて同じ球面上の平面に含まれている事から、
このようにベクトルODを表す事が出来ます。ここで左右のベクトルの大きさ(ノルム)を計算すると:
こんな感じでODに掛け算される係数aが出てくるので、点Dの座標は、
と算出できます。
点Dの座標が出たので、三角形の高さである線分CDの長さを求められます:
CDは円弧なので、∠CODをα(ラジアン)とすると、
です。∠COD=αはベクトルODとOCが成す角度その物なので、内積の性質から、
と展開できます。斜辺と同様に高さCDの長さを6cmと仮定し、上のα及び先に求めたβで表された半径rの式をCDの式に代入すると、
このようなθの方程式が出来上がります。これを満たすθが存在すれば、斜辺が10cmで高さが6cmの球面直角二等辺三角形が存在する事になります。残念ながらこの方程式を解析的に解く事は多分出来ません。そこで、数値解析で解いてみると…ありました!θ=0.831917602688206、約47.66度にすると、上の方程式が成り立ちます。そのθで各パラメータを求めると、α=0.660033、β=1.100054、球の半径r=9.09046となりました。ここで求めたθは後で面積を求める時に使います。
③ ∠CABを求める
※ 下記の計算について2021.8以前の式に誤りがある事が分かりました(法線Nの計算で分子に余計なsinθが入っていた)。現在は正しい式に修正しております。
②までの導出で、どうやら斜辺が10cmで高さ6cmとなる球面直角二等辺三角形が存在する事が分かりました。θや半径rがあるので点A及び点Bの座標も具体的に求められます。となると後は「球面三角形を成す3つの頂点がある時の面積の求め方」さえ分ればゴールです。
球面三角形の面積の求め方は良く知られていて、以下の式である事が分かっています:
Sは面積、∠A,B,Cはそれぞれの角度(ラジアン)です。この式の導出については、例えばこちらのサイト(高校数学の美しい物語:球面上の三角形の面積と内角の和)をご参照下さい。今∠Cはπ/2(90度)である事は分かっていて、また∠Aと∠Bは図形の対称性より同じ角度です。よって∠A=∠CABさえ求まれば面積Sを算出できます。
∠Aは点Aを通る二つの平面AOC及びAOBが成す角度です。2つの平面によって作られる角度(鋭角側)は双方の法線の内積の絶対値から求める事が出来ます。2つあるうちの平面AOCの法線Mは極めて簡単で(1,0,0)です。点O、A、Cはいずれも平面YZに含まれているのでこれは自明。一方の平面AOBの法線NはベクトルOAとベクトルOBの外積より、
法線の方向としては括弧の部分だけでOKですが、長さを1に正規化する必要があります。ベクトルの長さは各成分の和のルートなので、欲しい法線Nは、
こういう感じになります。NとMの内積は、Mはx成分が1で後はゼロなので、
∠A及び∠Bをθから求める式が出来上がりました。
半径rは、②で導出したように、斜辺(hypoLen)とβから、
以上から球面直角二等辺三角形の面積Sは、
と展開でき、θ及び斜辺の長さhypoLenで求める事が出来ます。θは②の最後で具体例ありますように、以下の方程式、
を満たす値です。Heightは斜辺から直角へ延びる球面上の垂線の長さ(≒高さ)です。
④ 結論:斜辺10cm高さ6cmの球面直角二等辺三角形の面積は!
という事で、ようやく球面直角二等辺三角形の面積Sを求める式が出来上がりました~(^-^)/。②の最後に数値解析で求めたθと斜辺の長さ10cmをSの式に入れて、面積を求めてみると、
のようです!やったぜ!(>ω<)/
平面では不可能な三角形を球面では作る事ができる所から始まって、動画に上がっていた問題の答えの一つを導く事ができました。今回は話しを簡単にするために球面二等辺三角形に限定しましたが、球面上の不等辺な直角三角形でも多分斜辺が10cm、高さが6cmの物を作る事が出来ると思います。同じ条件で別の直角三角形が出来るというのも球面の面白い所ですね。
⑤ 謝辞
数式のミスをご指摘頂きました小田切様に感謝申し上げます。小田切様は同じ不可能直角三角形の問題(マイクロソフトの三角形)についてさらに詳しい検討をされております!トレビアンです(^-^)
MONEX ENGINEER BLOG
これ解けますか?(後編:マイクロソフトの三角形ありました)