○×的数学のお部屋
その5 sinθ=2を満たすθって?
高校の時に出てくるsin、cos、tanでお馴染みの三角関数。「何に使うんだ~?」なんてよく揶揄される対象だったりしますが、ゲーム製作や科学分野などでバリバリに使いこなす必要があります。なので、高校でちゃんと習得して下さいね(^-^)
所でsinθの範囲って-1~1でした。そう習いました。でも実はこの範囲では無いんです。「は?」と眉をしかめるかもしれませんが、大学数学ではこの範囲を軽々ピョーンと飛び越えるんです。いったいどういう事なのか、不思議で楽しい世界へ飛び込みましょう。
① sinθは-1~1の範囲だったはず
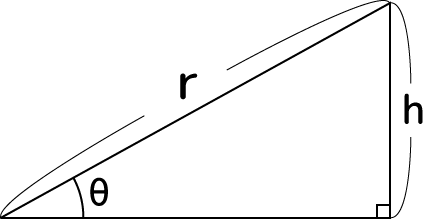
sinθは直角三角形の斜辺と一辺の比として定義されます:
こういう直角三角形があった時に、sinθは、
と定義されます。角θの対面の辺との比がsinθ、角θを挟む辺がcosθです。角度θは0~360度まで開く事が出来ますが、どうθを選んでもhはrより長くなれません。θが90度の時にh=r、つまりsinθ=1になるのが精いっぱいです。逆にθが270度の時、h=-r(符号付きになります)なのでsinθ=-1が最も小さい値になります。以上からsinθは、
である訳です。
…こうなると、どう考えてもsinθ=2なんてあり得ない事になります。だって図形的にありえないじゃんと。
② オイラーの公式が三角関数と指数関数を美しく結ぶ
上の定義はすべて実数の世界でのお話でした。私達が実感できる数値である実数の範囲であれば、確かにsinθは-1~1の範囲しか取れません。でも、実数よりも広い世界である「複素数」まで概念を広げると、この範囲をパーンと飛び越える事が出来てしまうんです。
そういう感覚って実は高校生でももう経験しているはずです。例えば2次関数。解の公式でルートの中がマイナスになる場合、複素数が無い世界では「解無し」でした。でも複素数がある世界ではちゃんと2つの虚数解が存在する事を示せます。複素数は実数をも飲み込むもっとも広い数の世界なのです。
では本題に入ります。
三角関数の公式の中で、とびぬけて美しいのが「オイラーの公式」です。オイラーは三角関数と指数関数が虚数を通して美しく関係している事を導き出しました:
初めて見る人は「何これ!?」と思うかもしれません。でもとても有名な公式で、あらゆる解析で利用されています。この証明には様々な方法がありますが、微分方程式を解く方法が高校生でも分かりやすいかなと思いますのでご紹介します:
〇 微分方程式を用いたオイラーの公式の証明
オイラーの公式の右辺を関数f(θ)とします:
これをθで微分します。ちなみに虚数の微分は虚数記号iを係数と同じように扱って構いません:
この両辺にiを掛けると、
と右辺に元の式が出てきました。この両辺にさらにiを掛けると、
こんな微分方程式が出来上がりました。これを解いてf(θ)を求めます:
積分定数Cは上のf(θ)にθ=0を代入すると求まります。f(0)=1から、C=ln(f(0))=ln(1)=0。よってexp(C)=1です。ここから、
とオイラーの公式を導けました。
オイラーの公式でθに-θを代入すると、
このようなsinの符号が反転した式が出来ます。この式とオイラーの公式を足し算するとsinが消えてcosのみになります。逆に引き算すると今度はcosが消えてsinだけになります:
という事で、実はsinθ、cosθは指数関数と虚数で表現する事が出来るんです。これが突破口となります。
③ 指数表現からsinθ=2となるθを求める
上で導いたsinθの指数表現。この右辺が2となるθがあるのか?やってみましょう:
わらわら~っと変形しているだけです。一番下の式でexp(iθ)をtと置くと、単純な2次方程式が出てきます:
tを解の公式で解くと…
こんな値になりました。tを戻すと、
このように対応する複素数がちゃんと算出されてきました。そう、sinθ=2となるθはあるんです!驚きですよね~、高校時の三角関数の概念がすっ飛んでしまいます。
④ 複素対数
上の式で自然対数の中に複素数が入っています。これは少し整理が出来ますのでここで紹介しておきます。
複素数はa+biなどと表現されますが、これは図示するとこんな位置になります:
横が実軸(Real axis)、縦軸が虚軸(Imaginary axis)です。いわゆる複素平面という表現の仕方です。もちろんこのままでも色々と面白い事が出来るのですが、これを極座標で考えると対数の表現が見えてくるんです。極座標は「点までの距離rと角度θ」で座標を表現します:
先程のa+biは極座標表現によってr(cosθ+isinθ)と表せる事が分かりました。この三角関数…これオイラーの公式そのものですよね。つまりこれはさらに、
このように指数関数で書き換える事が出来るんです。これを「複素数の指数表現」と言います。
指数と対数というのはとても相性が良い組み合わせです。上の式の両辺について自然対数を取ってみましょう:
対数内の掛け算は対数同士の足し算になりますし、自然対数内でeのべき乗があると対数を消せます。よって下段のように展開できます。これが複素数対数の展開公式です!元の複素数の係数で書き直すなら、
こんな感じになります。これを使ってsinθ=2となるθを展開してみましょう。
何とも不思議なもんですが、これがsinθ=2を満たすθです。
⑤ sinθ=Aの一般式を求める
では最後にsinθ=Aを満たすθを求める式、つまりarcsin(A)の式を求めてみます。sinθの指数表現から、
指数部をtに置き換えて、
2次関数の解の公式でtが求まります。ここから、
このようにsinθ=Aとなるθを求める一般式を導けます。この対数を展開するには複素数の実部と虚部が必要になります。ルートの中が正、つまり-1≦A≦1ならルートが実部、それ以外の範囲なら実部ゼロで他全てが虚部になります。
高校の範囲の普通のsinθ=Aである-1≦A≦1の場合は、
これは正に実数のみの角度の求め方ですよね。一方で|A|>1の場合はルートの中がマイナスになるので実部がゼロになります:
A=2を入れると先に計算した答えと一致するのが分かります。|A|>1だと必ず実部としてπ/2が固定で出てくるのが興味深いですよね~。
ではAに対応するθをプロットしてみましょう:
-1≦A≦1の時は実軸のみでプロットされていますが、|A|>1の所では実数部は±π/2(±1.57...)に張り付き、虚数方向にラインが伸びているのが分かりますね。高校の時はこのグラフの一部分しか見ていなかったという訳です。
こういう世界を垣間見せてくれるのが大学数学です。これにワクワクした高校生の皆さん、ぜひ大学で数学を学んで下さい(^-^)/