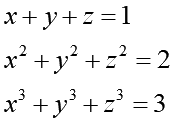
○×的数学のお部屋
その6 xn + yn + zn = ?
YouTubeで面白い数学の問題を多数アップして下さっているPresh Talwalkarさんの「Mind Your Decisions」。お気に入りのチャンネルの一つです。こちらで上がっていた問題(Solve If You Are A Genius (Only 1% Can))が面白かったので紹介します。高校数学の知識があれば十分に解けますので、ご興味がありましたらリンク先動画や以下の解答を見る前に是非チャレンジしてみて下さい(^-^)
〇 問題
の時、
はいくつになるでしょうか?
未知変数はx,y,zの3つで、方程式も3つあるので、このx,y,zは原理的に何らかの組み合わせで一意に求まります(組数は沢山あります)。でも、ゴリ押しで求めるのは多分無理。なので、別の方法を考える必要があります。
以下リンク先動画を参照した解答となります。
① 多項式展開の一般化
上の式を次のようなpnと表現するとします:
この表現が後でガツンと利いてきます。
次に、各変数を用いた次のような多項式を考え、それを展開します:
この展開式の各係数e1〜enはどういう形になるのでしょうか。
tn-1の係数e1は、-xiが一つ選択されて、残りn-1個tが掛け算されるので、
となります。e2は-xiと-xjの2つを選択し残りがtなので、
このように取りうる2つのxiの掛け算の和になります。この後の係数emも同様で、取りうるm個のxiの掛け算の和で表現されます。
上のf(t)のtにx1を代入すると、右辺の(t-x1)がゼロになるためf(x1)=0になります。同様にt=x2でもt=x3でも全部ゼロ。これをx1〜xnまで繰り返して、全部足し算してみます:
これより、
一番下段に注目です。この計算の結果pnと係数eのみの美しい関係が導けました!この式を利用すると、冒頭の問題は芋づる式に簡単に解けてしまいます。
〇 n = 1の時
〇 n = 2の時
〇 n = 3の時
〇 n = 4の時
e4ですが、今回はx、y、zの3つしか変数が無いためe4はゼロです。これはf(t)の式を見てもゼロにしないといけない事が分かります。よって、上の式から、
e4同様に以降の係数e5〜enも全部ゼロです。
〇 n = 5
今回の問題の答えになるp5は、
という事で答えは「6」でした。以後pn-2、pn-1、pnの3つがあれば次のpn+1が算出できる事が分かりますね。漸化式は次のようになります:
こんなスッキリとした式で先の先まで算出していけるのですから素敵です(^-^)。ただし、この漸化式は残念ながら綺麗な形では解けません。大分頑張ってみたのですが、3次方程式を解く必要があり断念しました。
Presh Talwalkarさんの「Mind Your Decisions」は他にも沢山面白い問題がありますので、また良さそうな物があればここで紹介したいと思います。