ホーム < ゲームつくろー! < Programming TIPs編
その18 乱数あれこれ
ゲームではあまり乱数を使ってはいけないと言われますが、そうは言っても乱数が無いと面白くないのもまたゲーム。そんな乱数についてのTIPSです。
① 円内均一乱数
ある円の中に点をランダムに穿ちたい事が結構あります。円と言うと半径と回転角度、いわゆる極座標で表現すると楽ですが、単純に、
r = rand() * radius;
angle = rand() * 2 * 3.141592f;
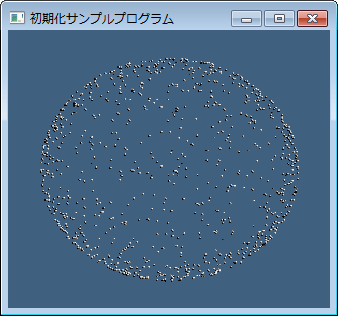
のようにするとこれは中心に近い座標ほど高確率で取得される不均一な円内乱数になってしまいます:
こうではなくて、例えば半径1の円周に点が10個あるとした時に、半径2の円周に点が20個あると均一密度になりますよね。つまり、半径2の円周の方が半径1の円周よりも2倍選択されやすければ、後はその円周状のどこか1点を選ぶだけで円内均一乱数となります。
半径に対する円周の選択されやすさをグラフ化するとこうなります:
このままだと実はあまりうまく使えないので、グラフの下部分の面積が1になるように、[グラフの値]/[面積]という計算をしてあげます。すると上のグラフは、
となります。見た目変わっていませんが、縦軸のスケールが倍になっていて、グラフの下部分の三角形の面積は1になっています。こういう「面積が1のグラフ」は「確率密度分布」という名前が付いています。特に上のような三角形の形をしているものは「三角分布」と呼ばれます。
さてさて、この確率密度分布は横軸xについて「a<= x <= bの範囲の面積」を求めるとその値が取られる確率が出てくると言う便利なものなんです。例えば、円周0.2〜0.4までが取られる確率は、上の場合は台形の面積の求め方になって、
p(0.2〜0.4) = (0.4 + 0.8) * 0.2 / 2 = 0.12 = 12%
となります。グラフの面積というとこれは積分のお話です。上のグラフの場合、
f(x) = 2x
という式になっているので、面積を求める不定積分の式は、
F(x) = ∫2x dx = x^2 (0≦x≦1)
と2次関数になる事がわかります。例えばx=aとするとF(a)は0≦x≦aという範囲が取られる確率となります。一般には-∞≦x≦aという範囲が取られる確率を求める事ができるF(x)のような式を「累積確率密度関数」と言います。
上の三角分布の累積確率密度関数は次のような2次関数のグラフになります:
さて、今多分私達が持っている生成可能な乱数は一様乱数です。その一様乱数から上のような確率密度に従うような値を取りだすにはどうしたら良いでしょうか?これ、上の累積確率密度関数のグラフを見ると一発で実はわかります。累積確率密度関数の縦軸は確率で、必ず0〜1に向かう右上がりのグラフとなります。この確率をランダムに選択し、それに対応する横軸の値を取ると、それがそのまま偏りのある乱数生成になってしまうんです:
これは数学では「逆関数を求める」という作業になります。上のF(x)=x^2の逆関数Finv(x)は解析的に解く事ができて、
となります:
このグラフは横軸が0〜1の一様乱数、縦軸が取るべき円周の長さとなるわけです。
ところで、円周の長さというのは半径に比例していて、2πrで求められるのでした。なので上のグラフの縦軸はそのまま半径と捉えても同じ事になります。
以上から、円内均一乱数を取得するには、
r = sqrt( rand() ) * radius;
angle = rand() * 2 * 3.141592f;
と半径を得る時にルートしてあげれば良いわけです(^-^)
均一だ〜(^-^)
② 角度限定球面均等乱数
例えば、ある方向を中心軸として放射線状に何かをばらまきたい事があるとしましょう。その時、ばらまく角度が限定していて、かつその角度内で均等にばらまきたいねぇと思うわけです:
こういう角度限定の球面均等乱数を考えてみます。
球面の座標を表す方法はいくつかありますが、極座標で表すと色々つぶしが利きます。上のような片面がざっくり切れた球を真横から見るとこんな感じになるかと思います:
あるθに対応したX軸上の点xを取る事ができて、後はその点xを中心としてYZ平面に平行な半径r(θ)の円の円周上のどこかの点を取ると球面上の1点を表す事ができます。式で書くと、
θ=rand() * m
r(θ) = sinθ
η = rand() * 2π
x = cosθ
y = r(θ) * sin(η)
z = r(θ) * cos(η)
となりそうです。mはθが取る最大角度で0≦m≦πです。η(イータ)はx座標が決まった後の円の中心からの任意な角度です。yz座標を決めるのに使うだけです。
一見するとこれで良さそうに見えるのですが、このままだと残念ながら不均一な分布になってしまいます。何故か?例えばθが1度くらいの時を想像してみて下さい。ηがどんな値であっても随分とX軸近辺に点が近寄ってしまします。円の半径が小さいので点が密であるわけです。一方θが90度くらいの時は円の半径が大きい分点が疎になってしまいます。つまり、円の半径が大きい所ほどより多く選択されなければ均一な分布にならないんです。この感覚は①の円内均一分布と似ていますよね。
では角度θに対する円の半径r(θ)をグラフにプロットしてみましょう:
これはm =120度を仮定したものです。横軸がθ(度)、縦軸がその時の半径r(θ)です。このグラフは、
r(θ) = sinθ (0≦θ≦m)
です。よって90度の時に一番多く選択されるような乱数を振れば球面一様になります。つまりこのグラフは確率分布になっているわけです。ここからは①と同じ作業をしていきます。
まず上のグラフを面積が1になる確率密度分布f(θ)に直します。その為には上の面積で縦軸の値を割り算すれば良いのでした。θが0〜m度の間での面積は定積分で表せるので、
と計算できます。分母がその面積です。式としてはグラフの縦軸のスケールが1-cos(m)倍になっただけです。このf(θ)をさらに積分すると、累積確率密度関数F(θ)が出てきます:
これをグラフ化してみます:
右肩上がりでθ=120度の所で確率1になっていますね。この累積確率密度関数の縦軸を一様乱数で取り、それに対応する横軸θを取ってあげると、半径r(θ)がうまい頻度で抽出される事になり、結果として球面一様乱数が得られると言うわけです。
F(θ)の逆関数Finv(θ)は次のように解析的に解く事ができます:
xは0〜1の一様乱数で、Finv(x)には0〜mまでの角度θが返ります。
以上から角度0〜mまでの放射角による球面一様乱数は次の式で求められる事がわかりました:
θ= acos( 1-rand() * ( 1- cos(m) ) )
r(θ) = sinθ
η = rand() * 2π
x = cosθ
y = r(θ) * sin(η)
z = r(θ) * cos(η)
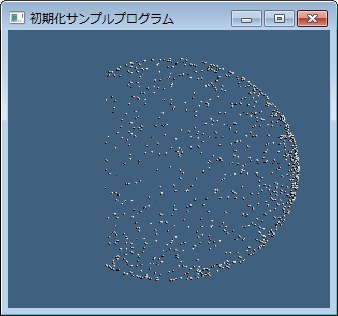
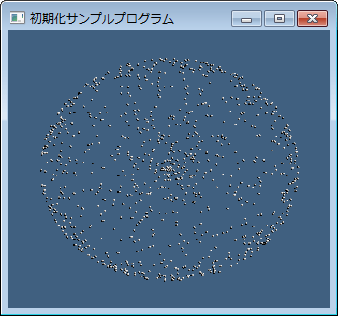
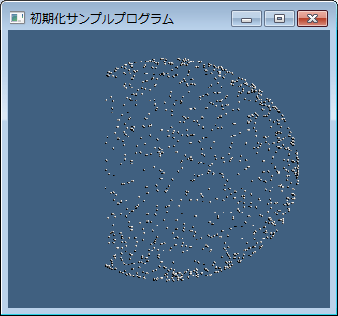
θを求める所だけが補正されているわけです。実際うまくいってるのかなぁと思いDirectXで描画テストしてみたのがこちら:
 |
 |
 |
 |
上行が補正前、下行が補正後で、左列がZ軸側から見た物で、右列が穴のあいているX軸側から見た物です。これを見ると補正前の分布は円半径が小さい所(右端)に点が集中しています。右列を見るとX軸を貫くあたりに密集しているのが分かると思います。一方補正後の下列は均一分布になっていて、右の図を見てもX軸周りに密集するような様子はありません(^-^)
ちなみに、角度を限定せず球面全体に均一に点をばらまく場合は、先のθを求める式が少し簡単になります:
θ= acos( 1-rand() * ( 1- cos(π) ) ) = acos( 1 - 2 * rand() )
r(θ) = sinθ
η = rand() * 2π
x = cosθ
y = r(θ) * sin(η)
z = r(θ) * cos(η)
ついでに、より一般的に下図のような前後を切る場合、
角度θに対する半径r(θ)の確率密度関数等は式だけ示すと、
となりまして、一番下段の逆関数がθを求める式となります。xが一様乱数です。なので、
θ= acos( cos(a) - rand() * ( cos(a) - cos(b) ) )
r(θ) = sinθ
η = rand() * 2π
x = cosθ
y = r(θ) * sin(η)
z = r(θ) * cos(η)
となります。
③ 三角乱数
値が大きくなるにつれて頻度が比例して減り、ある最大値以上は頻度0になる以下のような分布を「三角分布」と言います:
このグラフは0〜1の範囲で面積が丁度1になるので確率密度分布になっています。こういう偏りを持った三角乱数を作ってみます。
上のグラフから確率密度関数と累積確率密度関数は次のように導けます:
累積確率密度関数F(x)の逆関数は次のように算出できます:
最後の導きは皆大好き2次関数の解の公式です。2次関数なので解が2つ出てきますが、Finv(x)の範囲は0〜1なのでマイナス側のみ採用となります。
結果として、0〜1までの値を返す三角乱数は、
triRandom = 1.0f - sqrtf( 1.0f - rand() )
で得られます。rand()は0〜1までの一様乱数です。例えば50〜200までの値を三角乱数として得たい場合は、
val = 50 + ( 200 - 50 ) * triRandom
となるわけです。
④ 円形集中分布
ある点の回りに集中的に分布させたい事もあります。③の三角関数はx=0側程頻度が高いのである意味集中分布と言えます。
2Dの円の中心から外に向かうにつれて疎になるような集中分布乱数を作るのは簡単で、実は①でもう出てきています。最大半径をradius、中心角度θの極座標系で、
r = radius * rand()
θ = 2π * rand()
とすると自然と集中分布になります。その様子は①で図として示してあります。
半径rがより内側になるよう選択するには、一様乱数のべき乗を取るのが一つの手です。つまり上の式を、
r = radius * (rand())^n
θ = 2π * rand()
とするとさらに円の中心点に集中するようになります。以下にn=2,4,6,8,10,12乗で全く同じ乱数列によってそれぞれ点を200点穿った図を掲載します:
左上が2乗、右上が4乗、左真ん中が6乗と続きます。2乗と12乗(右下)を比べると同じ乱数列でも12乗の方がより中心点に寄っているのがわかります。①で導いたようにn = 0.5の時は丁度円形一様乱数になります。という事はn < 0.5にすると円周側により集中する面白い乱数にもなるわけです。
(2019. 5. 12追記)
⑤ 2次関数分布乱数
明確な最小値と最大値を持ち、その中央値が最大頻度となるような乱数が欲しい事が割とあります。正規分布乱数を使うと似たような事は出来るのですが、正規分布は出力される値が無限小〜無限大までなので最小値〜最大値という設定が出来ません。三角分布を使えばまぁ簡単に作れはするのですが(^-^;、ここでは2次関数を使ってチャレンジしてみます。
以下のような2次関数な確率分布を想定します:
最小値が0、最大値が1で最頻値(中央値、平均値)が0.5である確率分布です。上の2次関数は実は確率密度関数に既になっていまして、以下の式で表されます:
ここから累積確率密度関数F(x)は、
と算出できます。ここまでは簡単(^-^)。
さて、乱数化するにはF(x)の逆関数を求めなければなりません。つまり、
という3次方程式を解きます。3次方程式の解の公式はありますが、そのままだと「負数の累乗根」という頭がこんがらがる計算をしなくてはならなくなるため、別の作戦で攻めてみます。
3次方程式はx^2の項があると面倒臭いので「カルダノの方法」で用いられる変換を行い、x^2項を無くします。詳しくはWikipediaを参照頂きたいのですが、上のxを次のような式に置き換えて元の式に代入して整理すると、
下のyの3次方程式となります。ここでyの項をp、定数項をqとし、さらにp=-3a^2、q=-b*a^2と置き換えると、Wikipediaにある「ビエタの解」を用いる事が出来ます。ビエタの解は次の通りです:
これで3次方程式の解が計算できるのですから驚きです。先の式から、aとbは、
と計算できるので、ビエタの解に代入して一般式を得られます。nの値で解が3つ出てきますが、0≦y≦1に収まるのはn=2の時です:
F(x)の所に0〜1の乱数を振ると、2次関数確率分布に従った0〜1までの乱数が出力されます。後は最小値と最大値にスケールしてあげれば良いだけです。実際上式の乱数をExcelでシミュレートすると次のような頻度分布が得られました:
オレンジが理論値で青色のが10000個位サンプルした頻度分布です。大丈夫そうですね(^-^)