儂乕儉 < 僎乕儉偮偔傠乕両 < Programming TIPs曇
偦偺19 曗娫娭悢偁傟偙傟
丂僎乕儉惂嶌偺拞偱偼乽曗娫乿偑偁偪偙偪偵弌偰偒傑偡丅曗娫偲偼堦斒偵2偮偺抣偺娫傪攠夘曄悢t乮亖妱崌t乯偱昞偟偨傕偺偱偡丅椺偊偽僉儍儔僋僞偑抧揰A偐傜B傊堏摦偡傞帪丄帪娫偑宱夁偡傞偲彮偟偢偮B傊岦偐偄傑偡丅偙偺乽岦偐偄曽乿偼曗娫娭悢偵傛偭偰怓乆曄壔偝偣傞帠偑偱偒傑偡丅懠偵傕奊傪僼僃乕僪僀儞偝偣傞帪偲偐丄僄僼僃僋僩傪摦偐偡帪側偳丄幚偵條乆偱偡丅偦偟偰丄偙偺曗娫娭悢偵傛偭偰僎乕儉偺柺敀偝偺偐側傝側晹暘偑寛傑偭偰偟傑偆偺偱偡丅偙偺復偱偼丄偦傫側曗娫娭悢傪偁傟偙傟尒偰峴偒傑偡丅
嘆 慄宍曗娫
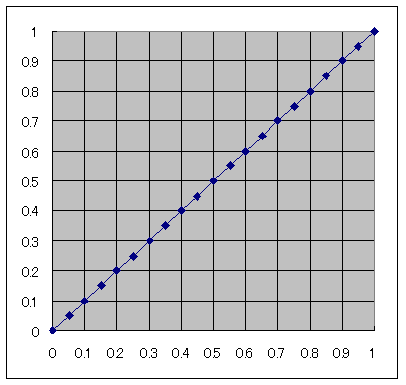
丂曗娫偱堦斣扨弮側偺偼慄宍曗娫偱偡丅偙傟偼2偮偺抣偺娫傪摍懍偱堏摦偡傞曗娫偱偡丗
墶幉偑攠夘曄悢t偱丄廲幉偑偦傟偵懳墳偡傞抣偱偡丅僌儔僼傪尒傞偲堦栚椖慠偱丄慄宍曗娫偺応崌偼t偲抣v偼堦弿偵側傝傑偡丅偮傑傝丄
偱偡丅惓偵慄宍(^-^)丅偙偺攠夘曄悢t偵懳偡傞v(t)偑乽曗娫娭悢乿偱偡丅
丂偱丄偙偺v(t)傪偳偆巊偆偐偑杮復偺娞偱偡丅t=0偺帪偺抣傪s丄t=0偺帪偺抣傪e偲偡傞偲丄曗娫抣I(t)偼v(t)傪梡偄偰堦斒偵師偺傛偆偵寁嶼偝傟傑偡丗
偙偺幃偼v(t)偺宍偑偦偺傑傑曗娫抣I偵斀塮偝傟傑偡丅偮傑傝丄慄宍曗娫偺応崌側傜s偐傜e偵岦偐偭偰摍懍偵抣偑曄傢偭偰偄偔帠偵側傝傑偡丅
嘇 2師娭悢曗娫
丂曗娫娭悢偼v(0)=0丄v(1)=1偲側傞傛偆偵娭悢傪慖傇偺偑僐僣偱偡丅嬋慄揑側曗娫娭悢偲偟偰傑偢嫇偘傜傟傞偺偑2師娭悢曗娫丅偙傟偵偼師偺2庬椶偑峫偊傜傟傑偡丗
惵偄僌儔僼偺曽偼丄t=0偐傜v偑備偭偔傝偲忋徃偟傑偡丅偙偆偄偆偺傪乽ease-in乿偲尵偄傑偡丅堦曽愒偄僌儔僼偺曽偼v(1)偺帪偵抣偑彊乆偵娚傗偐偵側傝傑偡丅偙傟偼乽ease-out乿偲屇偽傟偰偄傑偡丅乽ease乿偲偄偆偺偑乽娚傗偐偵乿偲偄偆堄枴側偺偱丄壗偲側偔嬫暿偱偒傞偐側偲巚偄傑偡丅
丂椉曽偺曗娫娭悢偼偦傟偧傟埲壓偺傛偆偵側傝傑偡丗
忋偑惵偄曽丄壓偑愒偄曽偱偡丅
嘊 3師娭悢曗娫
丂僎乕儉偺曗娫娭悢偲偟偰懡暘堦斣幚梡偝傟偰偄傞偺偑偙偺3師娭悢曗娫偱偡丅曗娫偺庬椶偲偟偰偼乽ease-in, ease-out乿偲側傝傑偡丅偮傑傝丄娚傗偐偵僗僞乕僩偟偰恀傫拞偱堦斣懍偔側傝丄嵟屻傕備偭偔傝偲側傞曗娫偱偡丅奆偝傫偑偍帩偪偺僎乕儉傪尒傞偲丄偁傜備傞強偱偙偺ease-in, ease-out側曗娫偑巊傢傟偰偄傞偺偑暘偐傞偲巚偄傑偡丗
偙偺傛偆側娭悢偼曽掱幃傪夝偔帠偱摼傞帠偑偱偒傑偡丅傑偢丄娭悢偼3師娭悢偱偡丅幃偱尵偆偲v(t)=a*t^3 + b*t^2 + c*t + d 偱偡丅僌儔僼偼尨揰傪捠偭偰偄傞偺偱d=0偼偡偖偵暘偐傝傑偡丅傑偨t=0偲t=1偱暯傜偵側偭偰偄傑偡傛偹丅偙傟偼旝暘學悢偑0偩偲偄偆帠偱偡丅v(t)傪t偱旝暘偟偨幃偼 v'(t)=3a*t^2 + 2b*t^2 + c 偲側傝傑偡偑丄t=0偱孹偒僛儘側偺偱丄c=0傕傢偐傝傑偡丅寢嬊忋偺幃偼丄v(t)=a*t^3 + b*t^2 偲偄偆帠偑傢偐傝傑偡丅t=1偺帪偵v(t)=1側偺偱丄1 = a + b丅偙傟偑1杮栚偺幃丅2杮栚偺幃偼旝暘幃偱t=0偺帪偵v'(1)=0乮孹偒僛儘乯側偺偱丄0 = 3a + 2b丅偙偺2杮偺幃傪楢棫曽掱幃偱夝偗偽丄a=-2丄b=3偑傢偐傝傑偡丅偮傑傝忋偺僌儔僼偼丄
偲偄偆帠偑傢偐傝傑偟偨丅偙傟丄暔惁偄巊偄傑偡丅
嘋 cos曗娫
丂ease-in, ease-out側傕偆堦偮偺曗娫偲偟偰cos曗娫偑偁傝傑偡丅偦偺柤偺捠傝cos僇乕僽傪巊偭偨曗娫偱偡丗
惵偄曽偑cos曗娫偱丄曗娫幃偼師偺傛偆偵側傝傑偡丗
cos偼0乣兾偺娫偱1乣-1傑偱悢抣偑摦偒傑偡丅1偐傜偦傟傪堷偗偽0乣2偲側傞偺偱丄偦傟傪敿暘偵妱傟偽忋偺傛偆偵側傞偲偄偆傢偗偱偡丅
丂僺儞僋怓偺曽偼3師娭悢曗娫偱偡丅偙傟傪尒傞偲傢偐傞傛偆偵丄椉幰偺娫偵杦偳堘偄偼偁傝傑偣傫丅3師娭悢曗娫偺曽偑庒姳ease姶偑柍偄偲偄偆姶偠偱偡偑乧懡暘杦偳傢偐傝傑偣傫(^-^;丅偙傟側傜丄晛捠偼寁嶼晧壸偑寉偄3師娭悢曗娫傪巊偄傑偡偹丅
嘍 曗娫娭悢偺巊偄曽
丂偙偙傑偱嫇偘偰偒偨曗娫娭悢傪幚嵺偵偳偆巊偆偺偐丠怓乆側強偵巊偊傞偺偱偡偑丄椺偊偽僉儍儔僋僞傪A抧揰偐傜B抧揰偵10昩偐偗偰堏摦偝偣偨偄偲偄偆椺傪尒偰傒傑偟傚偆丅
丂A抧揰偺嵗昗傪A(Ax, Ay, Az)偲偄偆3師尦儀僋僩儖偱昞尰偟傑偡丅B抧揰偼B(Bx, By, Bz)偱偡丅僎乕儉偼update儊僜僢僪偑枅僼儗乕儉屇偽傟傑偡偺偱丄儊僜僢僪撪偱慜夞偺僼儗乕儉偐傜偺嵎暘傪庢摼偟傑偡丅Unity偩偲Time.deltaTime偑偦傟偵奩摉偡傞偺偱妝偱偡丅
丂update儊僜僢僪偺拞恎偼椺偊偽偙偆側傝傑偡丗
void update() {
elapsedTime += Time.deltaTime; // 宱夁帪娫
float t = elapsedTime / 10.0f; // 帪娫傪攠夘曄悢偵
if ( t > 1.0f )
t = 1.0f; // 僋儔儞僾
float rate = t * t * ( 3.0f - 2.0f * t ); // 3師娭悢曗娫抣偵曄姺
Vector3 p = A * ( 1.0f - rate ) + B * rate; // 偄傢備傞Lerp
}
elapsedTime偑宱夁帪娫偱丄偦傟傪10昩偱妱傝嶼偡傟偽攠夘曄悢t偑嶼弌偱偒傑偡丅t偺斖埻偼捠忢0乣1偺娫側偺偱丄t偑1傪挻偊偨応崌偼僋儔儞僾偟傑偡丅偙偺t傪偦偺傑傑巊偊偽慄宍曗娫偵側傝傑偡偑丄偦傟偩偲僉儍儔僋僞偺摦偒偑婡夿揑側偺偱丄忋偺椺偱偼3師娭悢曗娫偵偟偰偄傑偡丅媮傔偨rate偱A抧揰偲B抧揰傪慄宍曗娫乮Lerp乯偟偰偁偘傞偲A偐傜B傊ease in, ease out側摦偒傪偟偰偔傟傑偡丅
丂曗娫偼杮摉偵椙偔巊偆偺偱丄忋偺傛偆側3師娭悢曗娫側偳傪娭悢壔偟偰偍偔偺傕庤偱偡丅椺偊偽丄
Vector3::Cube曗娫 static Vector3 Vector3::cube(
const Vector3 &A,
const Vector3 &B,
float min,
float max,
float elapsed
) {
elapsedTime += Time.deltaTime; // 宱夁帪娫
float t = ( elapsed - min ) / ( max - min ); // 帪娫傪攠夘曄悢偵
bool isOut = false;
if ( t < 0.0f ) {
t = 0.0f; isOuter = true;
} else if ( t > 1.0f ) {
t = 1.0f; isOuter = true;
}
float rate = t * t * ( 3.0f - 2.0f * t ); // 3師娭悢曗娫抣偵曄姺
return A * ( 1.0f - rate ) + B * rate; // 偄傢備傞Lerp
}
偙偆偄偆cube曗娫儊僜僢僪傪嶌偭偰偍偔偲捵偟偑棙偒傑偡丅
丂懠偺曗娫娭悢傕摨偠傛偆偵嶌傟傑偡偑丄堘偆偺偼rate傪媮傔偰偄傞1峴偩偗偱偡丅側偺偱丄偙偙偺晹暘偩偗奜偐傜屇傃弌偡僗僞僀儖偵偡傞偲偄偆幚憰傕偁傝偱偡丗
Vector3::lerp曗娫乮曗娫娭悢傪奜晹偐傜乯 static Vector3 Vector3::lerp(
const Vector3 &A,
const Vector3 &B,
float min,
float max,
float elapsed,
float (*func)(float) // 曗娫娭悢
) {
elapsedTime += Time.deltaTime; // 宱夁帪娫
float t = ( elapsed - min ) / ( max - min ); // 帪娫傪攠夘曄悢偵
bool isOut = false;
if ( t < 0.0f ) {
t = 0.0f; isOuter = true;
} else if ( t > 1.0f ) {
t = 1.0f; isOuter = true;
}
float rate = (*func)( t ); // 堷悢偺曗娫抣偵曄姺
return A * ( 1.0f - rate ) + B * rate; // 偄傢備傞Lerp
}
戞6堷悢偵func偑捛壛偝傟偰偄傑偡丅偙傟偼師偺傛偆偵巊偄傑偡丗
float cube( float t ) {
return t * t * ( 3.0f - 2.0f * t );
}
int main() {
Vector3 A( 0.0f, 1.0f, 2.0f );
Vector3 B( 3.0f, 5.0f, 7.0f );
float elapsed = 3.0f;
Vector3 pos = Vector3.Lerp( A, B, 0.0f, 10.0f, elapsed, cube );
}
偙傟偱2揰娫傪3師娭悢曗娫偡傞帠偑弌棃傑偡丅慄宍曗娫(linear)偲偐2師娭悢(easeIn)側偳傪嶌傟偽丄摨偠傛偆側屇傃弌偟偱暿偺堏摦傪幚尰偱偒傑偡丅偙傟偑傕偆彮偟恑曕偡傞偲丄偄傢備傞乽Tweener乿摍偺曗娫儔僀僽儔儕偑嶌傟傞傢偗偱偡丅
乮2017. 5. 30捛婰乯
嘐 僔僌儌僀僪曗娫娭悢
丂嘊偱嫇偘偨3師娭悢曗娫偼杮摉偵偁傜備傞強偱懡梡偝傟偰偄傑偡丅偨偩丄偙偺娭悢偼嬋慄偺宍偑姰慡偵屌掕偝傟偰偄傞偺偱丄椺偊偽乽傕偭偲嬋偑傝偑偒偮偄偺偑梸偟偄側偀乿偲朷傫偱傕3師娭悢偺悽奅偱偼傕偆尒偮偐傝傑偣傫丅偱偼傕偭偲崅師偺娭悢偱壗偲偐側傜側偄偐偲尵偆偲丄偙傟偑偦偆娙扨偱傕偁傝傑偣傫丅偦傕偦傕丄師悢傪忋偘傞曽岦惈偱偼僷儔儊乕僞偑憹偊偡偓偰旝柇側挷惍偑擄偟偄偺偱偡丅
丂嘊偺3師娭悢曗娫偺傛偆偵ease in out側嬋慄乮嵟弶備偭偔傝偱恀傫拞偁偨傝偱嵟懍丄廔傢傝偱傑偨備偭偔傝偵側傞乯偼乽S帤嬋慄乿偲屇偽傟傑偡丅幚偼S帤嬋慄偵偼3師娭悢埲奜偵傕偄偔偮偐庬椶偑偁傝傑偡丅偦偺拞偱桳柤側偺偑乽僔僌儌僀僪嬋慄乿偱丄師偺幃偱昞尰偝傟傑偡丗
偙偺娭悢偼學悢偑堦偮a偟偐偁傝傑偣傫丅偙偺抣傪曄偊偰僾儘僢僩偡傞偲偙傫側姶偠偵側傝傑偡丗
丂a偺抣偑1偺帪偼傁偭偲尒傎傏捈慄偱偡乮幚嵺偼傎傫偺傝偲僇乕僽偟偰傑偡乯偑丄抣偑戝偒偔側傞偲偳傫偳傫S帤搙崌偄偑嫮偔側偭偰偄傑偡丅偟偐傕偡傋偰偺嬋慄偑(0,
0.5)傪昁偢捠傝傑偡丅棟桼偼娙扨丄x=0傪幃偵戙擖偡傞偲a偺抣偵傛傜偢y=0.5偵側傞偐傜偱偡偹丅偦偟偰丄偦偺嫟捠揰傪拞怱偵揰懳徾偵側偭偰偄傑偡丅偙傟傕徹柧偼娙扨偱x=s偲x=-s傪戙擖偟偨幃y1偲y2傪嶌傝丄偦傟傪懌偡偲摎偊偑鉟楉偵1偵側傝傑偡丅偙傟偼x=s偺帪偺抣y1偵懳偟丄x=-s偺帪偺抣偑1-y1偵側傞帠傪昞偟傑偡丅傛偭偰揰懳徾偵側傞傢偗偱偡丅
丂徹柧偼偝偰抲偒丄偙偺嬋慄偺惈幙偼惓偵椪傫偩傕偺偵嬤偄偺偱偡偑丄x=-1傗x=1偺強偑奺嬋慄偲傕僶儔僶儔偺抣傪庢偭偰偄傞偨傔丄偙偺傑傑偱偼傗傗巊偄偵偔偄丅偦偙偱丄偙偺娭悢傪學悢a偵傛傜偢昁偢(x,
y) = (0, 0)丄(0.5, 0.5)丄(1.0, 1.0)傪捠傞傛偆偵曄宍偟偰傒傑偟傚偆丅
丂傑偢僔僌儌僀僪嬋慄偺桞堦偺嫟捠捠夁揰偱偁傞(0., 0.5)傪尨揰傪捠傞傛偆偵娭悢偺埵抲傪偢傜偟偰傒傑偡丅偙傟偼Y幉曽岦偵-1/2偩偗僆僼僙僢僩偡傞偩偗側偺偱丄幃偺嵍曈偵1/2傪懌偡偲幚尰偱偒傑偡丗
丂僔僌儌僀僪嬋慄傪尨揰懳徧偵偡傞偲y偺抣偵僗働乕儖傪妡偗傞偙偲偱嬋慄傪忋壓曽岦偵奼弅偝偣傞偙偲偑偱偒傑偡丅偙偺惈幙傪忋庤偔巊偊偽丄(x, y) = (-1, -1/2)偺強傪捠偡偙偲偑偱偒傞僗働乕儖偑懚嵼偱偒傞偼偢偱偡丅偦偆偡傞偲揰懳徾偺惈幙偐傜偦偺僗働乕儖偵傛傝(1, 1/2)傕摨帪偵捠傞偙偲偵側傝傑偡丅忋幃偺塃曈偵僗働乕儖抣s傪妡偗嶼偟丄(1,1/2)傪戙擖偟偰忦審偵姁偆s傪嶼弌偟偰傒傑偡丗
丂懳徧揑偱僔儞僾儖側s偑弌偰偒傑偟偨(^-^)丅偙偺僗働乕儖傪妡偗偨僔僌儌僀僪嬋慄偺幃偲僌儔僼偼偙傫側姶偠偱偡丗
(-1,-0.5)丄(0,0)偦偟偰(1,0.5)傪捠傞S帤嬋慄偵側傝傑偟偨丅
丂懕偄偰X幉曽岦偵1/2側僗働乕儖傪偐偗偰(-0.5, -1)丄(0.5, 1)傪捠傞傛偆偵偟偰傒傑偟傚偆丅偙傟偼x偺強傪2x偵偡傞偩偗偱偡丗
丂愭掱偲僌儔僼偺尒偨栚偼曄傢偭偰偄傑偣傫偑丄X幉偺栚惙傝暆偑愭掱偺敿暘偵側偭偰偄傞帠偵拲堄偟偰壓偝偄丅偙傟偱X幉曽岦偺暆偑1丄倄幉曽岦偺崅偝偑1偵側傝傑偟偨丅曗娫娭悢偲偟偰傎傏巇忋偑偭偰偄傑偡(^-^)丅
丂嵟屻偺巇忋偘偼偙偺僌儔僼傪X幉曽岦偵0.5丄Y幉曽岦偵0.5偩偗僆僼僙僢僩偟偰X幉媦傃Y幉偺斖埻傪偦傟偧傟0乣1偵偟偰偁偘傑偡丅偙傟偼x偺強傪x-1/2丄y偺強傪y-1/2偵偟傑偡丗
丂偱偒傑偟偨両偙傟偑S帤偺嬋偑傝嬶崌傪挷愡偱偒傞僔僌儌僀僪曗娫娭悢偱偡丅帋偟偵學悢a=1,2,4,8偵懳偡傞僌儔僼傪昤偄偰傒傑偡丗
偆傂傚乣丄鉟楉偵偳偺応崌傕(0, 0)乣(0.5, 0.5)乣(1,1)傪捠偭偰偄傑偡丅傕偪傠傫尦偺僔僌儌僀僪嬋慄偺惈幙偼庴偗宲偄偱偄傞偺偱(0.5, 0.5)偱揰懳徾側S帤嬋慄偱偡丅a偺抣傪戝偒偔偡傞傎偳S帤偺嬋偑傝嬶崌偑媫寖偵側傝傑偡丅寁嶼僐僗僩偵偮偄偰偼丄傋偒悢偑堎側傞exp娭悢偑2売強偁傞偩偗偱丄屻偼巐懃墘嶼偱偡偐傜尵偆傎偳掱抶偄栿偱傕偁傝傑偣傫丅廳梫側偺偼偁傞x偵懳偟偰嬋偑傝偺嫮偝傪挷惍偟偨堦堄偺y偑応崌暘偗側偳偣偢偵扨弮側寁嶼偱媮傔傜傟傞偲偄偆帠偱偡丅偙偺扨弮偝偐傜丄偙偺曗娫偼僔僃乕僟撪偱傕廫暘巊偊傑偡両乮幚偼僔僃乕僟偱挷惍壜擻側S帤嬋慄偑梸偟偔偰偙偺婰帠傪捛壛偟傑偟偨(^-^;乯丅幃傪傕偆彮偟惍棟偟偨傝僗働乕儖晹暘傪帠慜寁嶼偟偰偍偔側偳偡傞偲寁嶼僐僗僩傪壓偘傞帠傕弌棃傑偡丅
丂拲堄揰偲偟偰偼丄偙偺娭悢偼(0, 0)偺強偱X幉偲晄楢懕偱偡丅傑偨(1,1)偺強偱偼Y=1偲傕晄楢懕側偺偱埖偄偵偛拲堄壓偝偄丅墿怓偄慄偼楢懕揑偵側偭偰偄傞傛偆偵尒偊傑偡偑丄悢妛揑偵偼偳傟偩偗a偑戝偒偔側偭偰傕晄楢懕偱偡丅傑偨x<0偱偼0枹枮偵丄y>0偺斖埻偱偼1傛傝戝偒偔側傝傑偡乮-s媦傃1+s偵慟嬤乯丅惈幙傪棟夝偺忋偛巊梡壓偝偄丅
嘑 (0, 0)偲(1, 1)偱孹偒0偵側傞嬋偑傝挷惍壜擻側S帤嬋慄
丂嘐偱摫弌偟偨僔僌儌僀僪嬋慄傪棙梡偟偨S帤曗娫娭悢偼(0, 0)媦傃(1, 1)偱孹偒偑0偵偼側傝傑偣傫偱偟偨丅嘐偱傕廫暘幚梡惈偑偁傞偺偱偡偑丄偙偩傢傞側傜偽壗偲偐偦傟傜偺揰偱孹偒傪0偵偟偨偄丅偦偙偱丄嘊偺3師曗娫娭悢偲崌傢偣媄傪巊偭偰傒傑偡丅
丂3師曗娫娭悢偼x=0媦傃x=1偱孹偒偼0偵側傞偺偱偟偨丅偱偁傟偽乽僔僌儌僀僪曗娫娭悢偱媮傔偨抣傪X偲偟偰丄偦傟傪3師曗娫娭悢偵曻傝崬傔偽偄偄傫偠傖偹丠乿偲峫偊傑偟偨丅寢壥偼偙偪傜丗
丂偛婡寵(^-^)丅崱搙偼(0, 0)媦傃(1, 1)偱孹偒偑0偵側傝傑偟偨丅學悢a傪戝偒偔偡傟偽嬋偑傝偑媫偵側傞惈幙傕偪傖傫偲擖偭偰偄傑偡丅桞堦3師曗娫娭悢偑儀乕僗側偺偱a傪偳傟偩偗彫偝偔偟偰傕3師娭悢傛傝傕嬋偑傝傪彫偝偔偼弌棃傑偣傫丅偪側傒偵丄x偺斖埻傪峀偘傞偲偙傫側僌儔僼偵側傞傛偆偱偡丗
悢妛偭偰柺敀偄側偀乧