仜亊揑悢妛偺偍晹壆
偦偺1 嬃偒両惓N妏宍偺1捀揰偐傜懠偺捀揰傑偱偺慡慄暘偺愊偼N両
丂偙偺栤戣偵弌夛偭偨偺偼Twitter偱偟偨乮弌揟偼偙偪傜乯丅偁傑傝偵姶摦揑側偺偱仜亊揑悢妛偺偍晹壆偺戞1抏偲偟偰庢傝忋偘偨偄偲巚偄傑偡丅儕儞僋愭偵傕恾偑徯夘偝傟偰偍傝傑偡偑丄夵傔偰栤戣傪恾帵偟偰傒傑偡丗
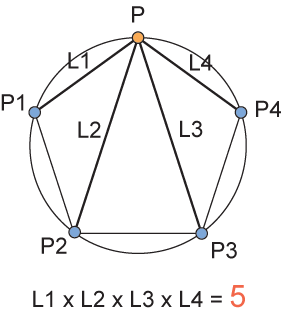
椺偊偽惓5妏宍偺応崌丅揤曈偺捀揰傪P偲偟偰巆傝偺捀揰傊懳妏慄傪堷偒傑偡丅偦傟傪偦傟偧傟L1丄L2丄L3丄L4偲偟傑偟傚偆丅偙傟傜偺挿偝傪偍傕傓傠偵慡晹妡偗嶼偟偰傒傑偡丅偡傞偲丄偦偺摎偊偑側傫偲曈偺悢偲摍偟偄乽5乿偵側傞傫偱偡両乽偆偭偦乕傫乿偲巚偆曽偺偨傔偵丄幚嵺偵曈偲懳妏慄偺挿偝傪媮傔偰専嶼偟偰傒傑偟傚偆丅
嘆 惓5妏宍偺曈偲懳妏慄偺挿偝
丂忋恾偺傛偆偵敿宎1偺墌偵撪愙偡傞惓5妏宍偺曈偺挿偝傪媮傔偰傒傑偡丅偄偔偮偐傗傝曽偼偁傝傑偡偑丄偙偙偼嶰妏娭悢偱峌傔偰傒傑偡丅壓恾傪偛棗偔偩偝偄丗
僆儗儞僕偱帵偟偨撪妏偼36搙偱偡乮佢POP1偑360/5=72搙偱偦偺敿暘乯丅偙偙偐傜愒偄慄暘偺挿偝偑sin36搙偱偁傞帠偑傢偐傝傑偡丅sin36搙丠旝柇側妏搙偺抣偱偡偑丄偙傟偼師偺傛偆偵幃偺宍偱媮傔傞偙偲偑偱偒傑偡丅
丂兤=36搙偲抲偒傑偡丅偡傞偲5兤=180搙偱偡丅偙偙偐傜3兤=5兤-2兤=180-2兤偲摍崋偑寢傋傑偡丅sin(180-2兤)偼崅峑悢妛偱弌偰偒偨壛朄掕棟傪巊偆偲丄
偲sin2兤偱偁傞帠偑傢偐傝傑偡丅偮傑傝丄
偱偡丅嵍曈懁傪3攞妏偺岞幃丄塃曈懁傪2攞妏偺岞幃偱揥奐偡傞偲師偺傛偆偵惍棟偝傟傑偡丗
偙偙偱cos兤=x偲抲偄偰丄偍側偠傒偺夝偺岞幃偱x偵偮偄偰夝偔偲丄
偲側傝傑偡丅cos36搙偼0傛傝戝偒偄偺偱+懁偑嵦梡偝傟傑偡丅偙偙偐傜媮傔偨偄sin36搙偼丄
偱偁傞帠偑傢偐傝傑偟偨丅愒偄慄暘偺挿偝偼惓偵偙傟偱偡丅偙偙偐傜5妏宍偺1曈偺挿偝偼偦偺2攞丄偮傑傝丄
偲嶼弌偱偒傑偡丅
丂懕偄偰懳妏慄PP2偺挿偝偼壓恾傪偛棗壓偝偄丗
愭傎偳偲摨偠傛偆偵愒偄慄暘偺挿偝sin72搙偑媮傑傟偽椙偝偦偆偱偡丅婐偟偄帠偵愭傎偳sin36搙傕cos36搙傕媮傔傑偟偨偺偱丄2攞妏偺岞幃偱偡偖偵媮傑傝傑偡丗
sin36搙偲旕忢偵傛偔帡偰偄傑偡偹丅儖乕僩偺拞偺晞崋偑堘偆偩偗丅偙傟傪2攞偟偨偺偑L2偺挿偝側偺偱丄
偱偡丅
嘇 曈偲懳妏慄暘傪妡偗傞両
丂偱偼媮傔偨惓5妏宍偺曈偲懳妏慄暘傪妡偗嶼偟偰傒傑偟傚偆丅PP1丄PP2丄PP3丄PP4偑偁傞帠偵拲堄偟偰乧丄
弌傑偟偨乽5乿両尒帠偵惓5妏宍偺応崌偼柦戣偑惉傝棫偪傑偟偨丅
丂偙偺柦戣丄惓3,4,6妏宍偺応崌偱傕惉棫偟偰偄傑偡丗
慺惏傜偟偄両僼傽儞僞僗僥傿僢僋偱偡(^-^)丅
丂偱偼丄惓7妏宍偼偳偆側偺偱偟傚偆偐丠惓8妏宍傗惓20妏宍偼丠惓3乣6妏宍偱惉棫偟偰偄傞偐傜偲尵偭偰偝傜偵愭傕惉棫偡傞偲偼尷傝傑偣傫丅偳傫側惓N妏宍偱傕惉傝棫偮偐偳偆偐傪徹柧偡傞偵偼丄偙偺偍榖傪堦斒壔偡傞昁梫偑偁傝傑偡丅偙偙偐傜偑嬃偒偺楢懕偱妝偟偄傫偱偡傛乣(^-^)
嘊 惓N妏宍偺懳妏慄傪慡晹妡偗傞偲偼丠
丂惓N妏宍偵偮偄偰忋恾偺傛偆偵捀揰傪掕傔傑偡丅偡側傢偪揤曈傪P偲偟偰嵍夞傝偵P1丄P2丄...丄Pn-1偲捀揰偵柤慜傪晅偗傑偡丅偙偺帪丄PP1偺挿偝乮L1乯偼壓恾偺傛偆偵掕媊偱偒傑偡丗
丂P1偼P偺偡偖偍椬偺捀揰側偺偱丄僆儗儞僕怓偺妏搙偼360搙乮2兾乯傪惓N妏宍偺乽N乿偱妱偭偨抣偵側傝傑偡丅偦偺偪傚偆偳敿暘偱偁傞椢怓偺妏搙偼兾/N丅偙偙偐傜愒偄慄暘偺挿偝偼sin乮兾/N乯偲側傝傑偡丅傛偭偰L1偼偦偺2攞偲側傞傢偗偱偡丅
丂師偵L2傪峫偊偰傒傑偟傚偆丗
丂僆儗儞僕怓偺妏搙偼愭傎偳偺挌搙2攞偵側傝傑偡丅摨條偵椢怓偺妏搙傕2攞偺2兾/N丅堭偯傞幃偵愒偄慄暘偼sin(2兾/N)偱丄L2偼偦偺2攞偩偲傢偐傝傑偡丅
丂偙偙偐傜丄偲偰傕偒傟偄側儖乕儖傪婰弎偱偒傑偡丅P埲奜偺捀揰偺揧偊帤偲sin偺拞偺妏搙偺攞悢偑懳墳偟偰偄傑偡傛偹丅偮傑傝P偲捀揰Pk傪寢傇懳妏慄偺挿偝偼丄
偲昞尰偱偒傑偡丅偨偩偟k=1,2,3,...,N-1偱偡丅偙偙偐傜丄乽偡傋偰偺揧偊帤偺挿偝傪妡偗嶼偡傞乿偲偄偆偺傪師偺傛偆偵昞偣傑偡丗
栧峔偊傒偨偄側婰崋乮儺乯偼兾偺戝暥帤偱丄擔杮岅偱偼乽憤忔乿偲屇傃傑偡丅偙傟偼乽儺偺忋壓偱昞偝傟偰偄傞揧偊帤偺斖埻暘慡晹妡偗側偝偄乿偲偄偆帠傪昞偟偰偄傑偡丅偙傟偺懌偟嶼斉偑奆偝傫偍側偠傒偺儼偱偡傛偹丅朻摢偺柦戣偼偙傫側偡偭偒傝偲偟偨幃偱昞尰偱偒偰偟傑偆傢偗偱偡丅
丂2sin(k * 兾/N)傪k=1偐傜k=N-1傑偱妡偗嶼偡傞偲偄偆帠偼丄2偑N-1夞妡偗嶼偝傟傑偡偺偱丄偦傟偼憤忔偺奜偵弌偣傑偡丅壓抜偺揥奐偼偦傟偱偡丅偙偙偐傜憤忔偺寢壥S偑N偵側傞偐偳偆偐傪帵偡偵偼丄
偱偁傞帠傪徹柧偡傟偽椙偄偲偄偆帠偵側傝傑偡丅
丂堦尒偡傞偲乽偙偙偐傜偳偆偡傞傫偠傖偄乧乿偲巚偆傢偗偱偡丅偩偭偰sin偭偰sin30搙偑1/2偲偐sin60搙偑併3/2側偳丄偁傞摿暿側妏搙偺帪偵幃偺宍偱昞尰偱偒傞偗偳丄忋偺応崌偼k * 兾/N偲偳偆尒偰傕幃偺宍偵弌棃側偝偦偆側宍丅庤媗傑傝側偺偐側乧偲丅偱傕丄偦傟傪懪奐偡傞惁偄揥奐偑悢妛偵偼偁傞偺偱偡丅
嘋 僆僀儔乕偝傫偼執戝偩両
丂sin偲偐cos偼昞尰偲偟偰偼偡偭偒傝偟偰偄傞偺偱偡偑丄擛壗偣傫揥奐偟恏偄暔偱傕偁傝傑偡丅強偑1740擭崰偵婬戙偺戝悢妛幰儗僆儞僴儖僩丒僆僀儔乕偝傫偑丄sin傗cos側偳偺嶰妏娭悢偲偄傢備傞帺慠懳悢偺掙乮e丗僱僀僺傾悢乯偺娫偺嬃偔傋偒娭學傪帵偟傑偟偨丅偦傟偑偙偪傜丗
乽i乿偼嫊悢偱偡丅壗偲丄cos兤偲sin兤傪i攞偟偨傕偺傪懌偡偲e偺i兤忔偵側傞偲偄偆杸鎑晄巚媍側惁傑偠偄娭學偑偁傞帠偑傢偐偭偨偺偱偡丅偙傟偼乽僆僀儔乕偺岞幃乿偲屇偽傟偰偄傞旕忢偵桳柤偱旤偟偄岞幃偱偡丅偵傢偐偵偼怣偠傜傟側偄偙偺岞幃丅乽側側側丄壗偱丠乿偲巚偆傢偗偱偡偑丄妱偲偡偭偒傝偲偟偨徹柧偑Wikipedia乮僆僀儔乕偺岞幃乯偵偁傝傑偟偨偺偱敳悎偟傑偡丗
偲偄偆幃傪偍傕傓傠偵嶌傝傑偡丅偙偺椉曈傪兤偵偮偄偰旝暘偟傑偡丅塃曈偼乽愊偺旝暘乿偲偄偆崅峑偺旝愊偱弌偰偒偨旝暘偺暘夝懃傪揔梡偱偒傑偡丅傢偝傢偝偲揥奐偟偰偄偔偲乧丗
鉟楉偝偭傁傝僛儘偵側偭偰偟傑偄傑偟偨(^-^)丅幃傪旝暘偟偨傜僛儘偵側傞丅偙傟偼乽f(兤)偑偳傫側兤偺抣偱傕堦掕偺掕悢偵側傞乿帠傪帵偟偰偄傑偡丅偦偙偱兤=0傪f(兤)偵戙擖偡傞偲丄
偦偺掕悢偑1偱偁傞帠偑寁嶼偱偒傑偟偨丅偙偙偐傜丄
偲偄偆娭學偑傢偐傝傑偡丅偙傟偩偗偱傕偡偱偵嬃湵偱偡傛偹丅偙偺椉曈偵偝傜偵cos兤+isin兤傪妡偗傞偲丄
偲僆僀儔乕偺岞幃傪摫偔帠偑偱偒傑偡丅
丂偙偺岞幃偵傛偭偰丄嶰妏娭悢偼巜悢娭悢偺幃偱寁嶼偑弌棃傞傛偆偵側傝傑偟偨両懾偭偰偄偨揤婥偑堦婥偵僗僢僉儕偲惏傟搉偭偨姶偠偱偡(^-^)丅忋偺摫弌偱弌偰偒偨幃偐傜丄
傕尵偊傑偡丅僆僀儔乕偺岞幃偺偪傚偭偲堘偆僶乕僕儑儞偱偡丅偙偺幃偲僆僀儔乕偺岞幃傪懌偟堷偒偡傞偲乧丗
sin兤傗cos兤偦傟偧傟傕巜悢娭悢偱昞尰弌棃偰偟傑偆傫偱偡丅傕偆嬃堎揑偲偟偐尵偄傛偆偺柍偄娭學偱偡丅偙偙偐傜嘊偺嵟屻偵摫偄偨sin偺憤忔傪偝傜偵揥奐偟偰悇偟恑傔偰傒傑偟傚偆丅
嘍 sin(k*兾/N)傪昍夝偔
丂忋偺sin兤偺幃偺兤偵k*兾/N傪戙擖偡傞偲丄
偲側傝傑偡丅傫乕乧偙偺傑傑偩偲傑偩壗偲傕偱偡(^-^;丅偦偙偱丄
偲掕悢側強傪兛偲抲偄偰偁偘傞偲丄忋幃偼丄
偲偪傚偭偲尒傗偡偔側傝傑偟偨丅偙偺幃傪偝傜偵師偺傛偆偵偪傚偭偲堘偆尒曽偵偟傑偡丗
偙偙偱丄撍慠偱偡偑椉曈偺愨懳抣傪庢偭偰傒傑偡丅偦偆偡傞偲傛傝偡偭偒傝偟偰偒傑偡丅嵍曈偼傑偀椙偄偲偟偰丄栤戣偼塃曈丅乽暋慺悢偺愨懳抣偭偰壗丠乿偲偄偆榖側傫偱偡偑丄偙傟偼偙偆偄偆掕媊偑偁傝傑偡丗
嵍曈偼偄傢備傞暋慺悢丅偙偺愨懳抣偼忋偺傛偆偵尦偺暋慺悢偲乽嫟栶暋慺悢乿偲偄偆嫊悢懁偺晞崋偑斀揮偟偨暋慺悢偲偺妡偗嶼偱昞尰偝傟傑偡丅寢壥偲偟偰偼幚悢晹偲嫊悢晹傪昞偡抣(a,b)偺傋偒忔傪懌偟嶼偟偨抣偺暯曽崻偲側傝丄偙傟偼乽暋慺暯柺忋偺嫍棧乿偲偄偆奣擮偵側傝傑偡丅塃曈懁偺愨懳抣傪庢偭偰傒傑偟傚偆丗
妡偗嶼偵側偭偰偄傞晹暘偺愨懳抣偼暘妱偱偒傞偺偱丄偙偺傛偆偵傁傜傁傜偲夝偄偰偄偗傑偡丅兛^(-k)偺愨懳抣偑1偵側傞棟桼偼埲壓偺捠傝偱偡丗
愨懳抣偺拞偑鉟楉偵1偵側傞傫偱偡(^-^)丅
丂偝偰丄偙偙偱k偺斖埻傪揔梡偟偰傒傑偡丅崱k偼惍悢偱k=1,2,3,...,N-1偱偡丅嵍曈偺sin偺拞偼偙偺帠偐傜0埲忋1枹枮偱偡丅偲偄偆帠偼丄偙偺斖埻偱sin偼昁偢僾儔僗偲偄偆帠偵側傝傑偡丅偮傑傝嵍曈偺愨懳抣偼偦偺傑傑奜傟傑偡丗
偝丄偲偄偆帠偱偙偺幃傪憤忔偵偡傞偲偙偆側傝傑偡丗
暘曣偵拲栚偱偡丅弌傑偟偨両2^(N-1)丅嘊偺嵟屻偱亀憤忔偺寢壥S偑N偵側傞偐偳偆偐傪帵偡偵偼丄
偱偁傞帠傪徹柧偡傟偽椙偄亁偲摫偒傑偟偨丅偦偺堦抂偑尒偊偰偒偰偄傑偡偹丅偁偲偼暘巕懁偑N偵側傟偽偙偺復偺昞戣偼恀偱偡丅
嘐 旝暘偺柇媊
丂暘巕懁偼壥偨偟偰N側偺偐丠偦傟傪摫偔偨傔偵丄師偺傛偆側曽掱幃傪帩偪弌偟傑偡丗
偼偄丠偲偄偆姶偠偱偡偑丄偙偺椉曈傪x偱旝暘偡傞偲慺揋側帠偑婲偙傝傑偡丅幚嵺偵旝暘偟偰傒傑偟傚偆丗
嵍曈懁偼栤戣偁傝傑偣傫丅塃曈懁偼妡偗嶼偝傟偰偄傞幃傪旝暘偡傞偲偒偺椺偺暘夝懃偑揔梡偱偒傑偡丅偙偺帪(x-1)'偲妡偗嶼偝傟傞僌儖乕僾偲丄(x-1)偲妡偗嶼偝傟傞僌儖乕僾偵戝暿偝傟傑偡丅(x-1)偺曽偑戝検偵偱偒傞偺偱偡偑丄忋偱偼偞偭偔傝偲徣棯偟偰偄傑偡丅壗屘偐偲偄偆偲丄偙偺忋偺幃偱x=1傪戙擖偡傞偺偱偡丅偡傞偲丄x-1偼0偱偡偐傜丄忋偺徣棯偟偨晹暘偼偤乕乕傫傇0偵側偭偰偟傑偆偲偄偆傢偗丅偱丄x=1傪擖傟傞偲偳偆側傞偐乧丗
弌偨偀両弌傑偟偨丄N丅惁偄旤偟偝偱偡傛偹偉丄姶摦偟傑偡傛偹偉(^-^)丅嘍偺嵟屻偺幃偼丄忋偺寢壥偐傜暔偡偛乕偔鉟楉偵側傝傑偡丗
偱偼丄嵟屻偺巇忋偘偱偡丅
嘑 惓N懡妏宍偺曈偲懳妏慄偺愊偼N両
丂惓N妏宍偺偁傞捀揰偐傜寢傋傞曈偲懳妏慄傪慡晹妡偗嶼偡傞幃偼嘊偺嵟屻偱丄
偱偁傞帠傪帵偟傑偟偨丅偙偺幃偐傜乽2乿傪奜偵弌偡偲嘐偺嵟屻偺幃偑弌偰偒傑偡丅偦傟傪戙擖偡傟偽丄僼傿僯僢僔儏偱偡両
旤偟偔僼傿僯僢僔儏偱偡(T仱T)/丅偙傟偱偳傫側惓懡妏宍偱傕懳妏慄偺愊偺寢壥偼偦偺曈偺悢偱偁傞N偲摍偟偔側傞帠偑傢偐傝傑偟偨丅恎嬤側惓懡妏宍偵偁傞旤偟偄娭學乧姶摦偱偡丅
丂埲忋偺徹柧偼Web忋偵嶶傜偽傞忣曬傪挷傋傑偲傔偨傕偺偱偡丅偨偩乽側偤丠乿偲巚偆強偼偳傫偳傫孈傝壓偘傑偟偨丅僆僀儔乕偺岞幃偼宍偼抦偭偰偄傑偟偨偑丄崱夞摫偄偰傒偰乽傎乣乿偲擺摼偟偨堦偮偱偟偨丅堦偮偺栤戣傪夝偔偺偵巊偆偦偆偄偆庫嬍偺岞幃傕傑偨悢妛偺旤偟偝偱偡傛偹丅