○×的数学のお部屋
その2 極値を求めるラグランジュの未定乗数法
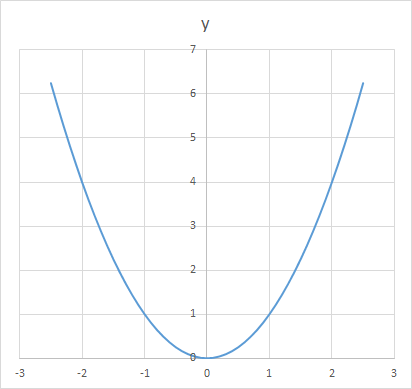
ラグランジュの未定乗数法(Method of Lagrange multiplier)はフランスの数学者ジョゼフ=ルイ・ラグランジュさん(1736-1813)の名前が付いた「最適化」に関する一つの手法です。何をするかというと「関数の極値」を求めます。極値と言えば高校の数学で習ったアレです。ちょっと復習してみます。例えば、
二次関数ですね。この関数の極値はグラフを見ると一目瞭然でx=0の時に与えられます。この場所を数学の手法で見つけるには、まずyをxで微分した式を求めます:
そしてこの式が0になるxが極値になります(正しくは極値の候補)。至極簡単(^-^)
上の二次関数は変数が一つ(x)の関数ですが、世の中には変数を複数持つ関数もあります。例えば、
これは変数がxとyの2つあってその結果がf(x, y)という数値になる関数です。この関数はどんな形をしているかというと、与えられたxとyの座標を足し算した点の集合ですから、傾いた平面になります:
この為だけにグラフ描くソフト作ったぜ、ふふふ…
この平面f(x, y)には残念ながら極値がありません。どこまで行っても平ら(地面と平行な所)にならないのですから。数学的にはxとyそれぞれの偏微分が0になれば極値候補を調べられますが、f(x, y)の偏微分は、
と定数なので極値が存在しない事が分かります。
さてこの永遠に続く坂道、x,yがどこまでも行けるから極値が無い訳です。ではもし「行ける範囲が限定されていたら」どうでしょうか?例えば、
という半径が1の円上しかx,yが動けないと制約してみましょう。つまり、坂道上に投影された円上のみが値として有効になった訳です:
この赤い円上には極値が存在します!赤円の右上で坂道を登り切るのでそこが最大値、逆に左下が坂を下りきった位置になるので最小値です。ちなみに最大値及び最小値の時の変数はx = y =± √2 / 2(符号同順)です。
極値が存在しなかった坂道に制約条件を加えると極値が出現しました。円の位置が変われば極値も変わります。本章で取り扱うラグランジュの未定乗数法は、このような元の関数f(x)に対し何らかの制約条件g(x)=0を与えた時に現れる極値を求める手法です。
① 2変数関数で具体的に見てみましょう
ラグランジュの未定乗数法はまず実際に試してみた方がとっかかりが良いかなと思います。幾つか例を挙げてそのプロセスを体感してみましょう。
冒頭に挙げた関数を改めて、
と2つの変数x1,x2で定義します。この段階ではx1とx2は自由な値を取れる変数なので、関数fに極値はありません。一方その自由を邪魔する束縛条件を、
と関数gで表すとします。関数fと違い関数gは制約の為に方程式の形になっている事に注意して下さい。先程も図示したように、この制約条件はx1,x2を半径1の円上に制約します。ラグランジュの未定乗数法は元の関数fと制約条件を表す関数gから次のような新しい関数Fを作ります:
「な、な、いきなり何だ?」と困惑するかもしれませんが、実はこの関数が実に素晴らしい働きをしてくれますので、今はそういうもんなのねと飲み込んでおいて下さい。注目するのは関数gに変数λ(ラムダ)が掛け算されている所です。このλの事を「未定乗数」と言います。今は謎のこの変数λの正体も追々判明していきます。λが追加されたので、関数Fはλ、x1、x2と3変数を持つ関数になります。
次に関数Fが持っている変数λ、x1、x2で関数Fを偏微分し、それらの式がすべて0だとしてしまいます:
偏微分した式が3本、そして関数Fにある未知の変数は3つ。という事は、そう、連立方程式を解くと上の3本の式を満たすλ、x1、x2が定まります。そして驚くべきことに、そのx1、x2が極値(の候補)になっているんです!「何で!?」と思う訳ですが、それは章の後半で説明します(^-^)。
実際に連立方程式を解いてみましょう。2本目と3本目の式から、
ですからこれを1本目の式に代入すると、
とλが算出できました。ここから、
(符号同順)
が出てきました。実際にf(x1,x2)とg(x1,x2)=0を重ねた図を見てみると…、
図は白い方ほどf(x1,x2)の値が大きい事を意味しています。赤い円がg(x1,x2)=0をf(x1,x2)に投影した物です。赤い点が極値で円の丁度斜め45度、円の半径は1なので、お~~~ちゃんと先のx1,x2の座標になっています!
このようにラグランジュの未定乗数法を用いると、制約条件付きの極値が連立方程式の解として出現します。面白くて不思議な手法です。
② 多変数関数(1束縛条件)でも同じ
考え方は変数の数が3個、4個、…N個と多変数に増えても同じです。束縛の無い関数を、
とします(別に線形に足すだけじゃなくても何でも良いのですが分かりやすいので(^-^;)。関数fは3次元の空間の1点の値を表しています。例えるなら、お部屋の中にX1,x2,x3軸を作ったとして、軸の方向に行く程気温が高くなるような状態です。束縛関数は、
という半径が1の球体の表面だとしましょう。この球体の表面の中で温度が最も高くなる(低くなる)場所が極値です。
①と同様の手順で進めてみます。まずは関数Fを作りましょう:
で、この関数Fを変数λ,x1、x2、x3それぞれで偏微分し、その答えを0とします:
式が4本、変数も4つなのでこの連立方程式は解く事ができます。2~4本目の式から、
これらを1本目の式に代入してラムダを算出すると、
となり、ここから、
(複合同順)
とめでたく解が出てきました。これは丁度お部屋が立方体だとして、その中心から温度が高くなっている(低くなっている)方の角へ向かって進み半径1の球の表面とぶつかった点です。ん~確かに極値です。
③ 多変数関数で束縛条件も複数ある場合
ラグランジュの未定乗数法は束縛条件が複数ある場合でも同様の手順を踏めるのが面白い所です。②の束縛条件として例えば、
という2種類の条件を同時に満たす極値を求めてみます。関数g1はx1x2平面に平行な半径1の円、関数g2はx2x3平面に平行な半径1の円で、関数fは3次元の空間なので、束縛条件は2本の同じ径を持つ円柱面が直角に重なった所となります。って、んー、イメージし難い…(-_-;;。多分こんな感じです:
この赤い線分(裏も同様)が制約部分となります。
束縛条件が複数になった時の関数Fは次のように束縛条件ごとにλ1、λ2と変数を設けて関数fから引き算します:
この後の手順も一緒で各変数について偏微分し答えを0とします:
ちょっとしんどいですが(^-^;、この連立方程式を解きます。x1、x2、x3はそれぞれこうなります:
また1本目の式から2本目の式を引き算すると、
ここにx1とx3を代入すると、
ここからλ1=λ2もしくはλ1=-λ2がわかるのですが、後者の場合(λ1+λ2)=0になるためx2が無限大に発散してしまいます。よってλ1=λ2=λ。これを1本目と2本目の式に再度突っ込むとこうなります:
ここから、
(複合同順)
が導けました。中々大変です(^-^;。ちなみに、これ本当に極値なのかを数値的に調べてみます。x1にほんの少し、例えば0.01程数値を足し引きした時のx1,x2,x3と関数fの値を見てみると、
真ん中の緑色の帯が極値です。上下でx1の値が極値から少しずれます。それに合わせてx2,x3の値も変わります(制約条件を満たす)。その結果がf列です。一番右列の値はf列の値について極値からの差を示しています。これを見ると極値がちゃんと最大値になっているのがわかりますね。凄いもんです(^-^)
④ なぜ極値が求まるのか?
さて、ここまでの計算例で確かにラグランジュの未定乗数法は制約条件を満たす極値を与えてくれました。狐につままれたような不思議な式。ラグランジュの未定乗数法はなぜ制約条件の下で関数の極値を求める事ができるのでしょうか?
この理由をイメージする時にキーワードとなるのが「勾配(Gradient)」です。勾配というのは坂道のきつさのようなイメージかもしれませんが、数学的には「ある点に注目した時、値がプラス側に最も大きく変化する方向での斜度」を意味します。またその方向を勾配ベクトルと言います。例えば簡単な例としてf(x) = x^2という放物線を考えてみます:
今x=1という位置にいるとしましょう(赤丸の位置)。この位置の勾配ベクトルはどの方向になるでしょうか?「値がプラス側に変化する方向だから、右斜め上かな?」とイメージされた方、気持ちわかります!でも、勾配ベクトルは「変数だけで表現する」という概念なんです。二次関数の変数はxだけで、f(x)は変数ではありません。よってx軸だけでその方向を表します。x=1の地点から見てよりf(x)の値が大きくなるなるのはX軸方向ですね。よってX軸と平行な右矢印がx=1での勾配ベクトルの方向となります:
でも、方向だけだとその勾配が「どれだけ急勾配か?」わかりませんね。x=1の勾配よりx=3の勾配の方がはるかに急です。せっかくベクトルがあるのですから、その長さで勾配の大きさを表すともっと便利です。
それをまるっと解決してくれるのが「微分」です。だって、微分って「変数がちょっと動いた時に値がどれだけ大きくなるか」でしょ。それって正に勾配です。そう、f(x) = x^2の勾配は、f(x)を変数xで微分すると自然に求まってしまうんですね。f'(x) = 2xですから、x=1の勾配の大きさはf'(1)=2。x=3の時はf'(3)=6となって、3倍急勾配であると分かります。
2変数関数の場合も考え方は一緒です。例えば
これは深皿のようなパラボラになります。この勾配ベクトルは変数であるX軸及びY軸の二つでその方向を表すことになります。勾配の調べ方も一緒で、ある地点(x, y)からX軸方向とY軸方向ににちょっとだけ動かしてみるとその地点の勾配がわかります。つまりxとyそれぞれの偏微分が勾配ベクトルの各成分になるんです。勾配って実に直観的(^-^)。実際パラボラの勾配ベクトルを描いてみるとこんな感じになります:
見事に放射状にベクトルが広がっていますね。そして中心からの距離に比例して勾配ベクトルが大きくなっています。
さて、では上のパラボラの(x ,y) = (1, 1)の位置にボールを置くと、ボールは(下向きに重力があるとして)どの方向に転がっていくでしょうか?もうお察しと思いますが、勾配ベクトルと反対の方向の斜面に沿って転がっていきます。反対になるのは勾配ベクトルが「より値の大きくなる方向」なのに対して重力は「より値の小さい方向」に引っ張ろうとするからです。重要なのは「勾配ベクトルが坂道の一番きつい方向を指している」という事実です。これがラグランジュの未定乗数法を導く一つの鍵となります。
勾配がゼロとなる所は極値の候補になります。傾斜が無いならそれは平らだからです。「候補」なのは全変数での偏微分がゼロでも天辺や底にならないケースがあるからです。例えばf(x) = x^3はその簡単な例で、xでの微分がゼロになるのはx=0の地点だけですが、ここは天辺でも底でも無いですよね(x<0の方にボールを押すと下へ転がり、x>0の方にはより高い位置がある)。単にx=0の所だけが「平ら」なだけです。こういう所は極値とは言わず「停留点」と呼びます。極値は停留点の特別なケースという訳です。
極値を含む停留点には一つ重要な共通項があります。それは「停留点にボールを置いてもボールは転がらない(動かない)!」という事です。だって平らなんですから。逆もまたしかりで、ある点に置いたボールが動かなければそこは停留点です。これ!これがラグランジュの未定乗数法を一気に導く二つ目の鍵となります。
さてさて、ラグランジュの未定乗数法には制約条件関数gがありました。これは上の例を踏襲して言うなら「ボールを置く位置を限定する」ものです。例えばg(x, y) = x + 2y - 3 = 0という制約条件だと、下図のようにパラボラ面上にある線上にしかボールを置けません:
このg(x, y)ももちろん変数xやyで偏微分出来ます。という事はあらゆるx,yについてg(x, y)の勾配ベクトルも定まります。ただしg(x, y)=0ですから、その勾配ベクトルはXY平面にある赤い線から伸びる矢印だけが意味を成します。これを見るとg(x, y)の勾配ベクトルが線に対して垂直な向きになっているのがわかりますね。勾配ベクトルが線分に対して垂直という事は、それに垂直な方向は線分の接線方向になる訳です。「勾配ベクトルに垂直な方向が接線だ」、この性質も鍵の一つです。
ここから注目。先ほどのパラボラなf(x, y)の勾配図とこのg(x, y)=0限定の勾配図を意味を成す線上で重ねてみます。すると、非常に興味深い事実が見えてきます:
パラボラをほぼ真上から見た様子です。地面に勾配ベクトルが描かれています。黒い矢印がパラボラの、赤い矢印が制約関数gの勾配ベクトルです。このパラボラの表面に球を置くとします。しかし球は赤い線で示したg(x ,y) = 0を満たすx,yの上しか置けませんし動けません。この線上の例えば下図の位置にボールを置いてみます:
もし何の制約も無かったら、ボールは黒い矢印で示した勾配ベクトルと反対方向にコロコロと転がっていきます。しかし今ボールはこの赤い線上しか動けません。ボールを置いた位置での赤い線の接線方向を青い矢印で示しています。見ると黒い転がる方向に対し接線が転がる方向側にやや寄っていますよね。すると、ボールは青い矢印方向にすすすっと転がろうとします。ボールが転がるという事は「そこは平らでは無い(=もっと値が小さくなる場所がある)」という事です。つまり赤い点の位置は極値(停留点)ではありません。では、下図の位置だとどうでしょうか?
ボールはf(x, y)の勾配ベクトルの反対である黒い矢印の方向に転がろうとしますが、動ける方向は相変わらず赤線の上だけです。そしてその赤線の接線(青い線)はこの地点をピンポイントで見ると「黒い矢印に対して垂直に」走っています。なぜ垂直かというと、この地点でのg(x, y)の勾配ベクトルがf(x, y)の勾配ベクトルと平行になっているからです。黒い矢印の方向に転がろうという力は、赤線の接線が垂直である為、赤線上の左右どちらにも分配されません。結局球は坂道も転がれず、赤い線上も動く事が出来ず、ここで完全にせき止められてしまいます。球が動かないという事は…そうここは「停留点」です!「f(x, y)の勾配ベクトルとg(x, y)の勾配ベクトルが平行になる点は停留点である!」というのが実感できるかと思います。
2つの平行なベクトルは、そのベクトルの成分の比が同になります。例えばベクトルv1=(1, 1)とベクトルv2=(2, 2)は長さが違うだけで平行ですよね。もちろんベクトルv3=(-3, -3)も平行です。数式で書くと2つのベクトルが平行というのは、
と定数λで比を表すと書けます。お、これみよがしに出ました「λ」(笑)。
f(x, y)の勾配ベクトル(勾配ベクトルは一般に∇(ナブラ)という記号で表します)は、その偏微分を成分とした∇f=(∂f/∂x, ∂f/∂y)、g(x, y)のそれは∇g=(∂g/∂x, ∂g/∂y)です。停留点ではこの2つのベクトルが平行なのですから、
です。これを各成分別に分けて書くと、
そして右辺を左辺に移項すると…、
どこかで見た気がしますよね。ここでラグランジュの未定乗数法で元の関数fと制約条件関数gから作っていたあの謎の関数F:
この関数Fをxとyでそれぞれ偏微分してそれをゼロだとすると…上の式がそのまんま出て来るではないですか!そうなんです、この謎の関数Fは上の偏微分の式を導出したい、言い換えると「f(x, y)の勾配ベクトルとg(x, y)の勾配ベクトルがx,yで平行になる=極値(停留点)だ」という事実を間接的に表していたんです。ただしx,yは制約条件g(x,y)=0の範囲でしか動けない。その条件は関数Fをラムダで偏微分した式、
で直接示されます。上の関数Fにこれらの条件が全部含められているのですから、ラグランジュの未定乗数法、凄い!
ちなみにλ(未定乗数)の値は∇f = λ∇g でわかるように、停留点でのf(x,y)及びg(x,y)の勾配ベクトルの大きさの比、つまりは傾斜の度合いの比です。方程式を解く時にだけ使う値ではありますが、これが極値である証なわけで趣き深い変数です。
⑤ ラグランジュの未定乗数法とビッグデータ解析
ラグランジュの未定乗数法は、実は色々な所で活躍しています。例えば昨今何かと出てくる「ビッグデータ」の解析。ビッグデータと言うのは文字通り「でっかいデータ」つまり物凄い多量なデータの塊を言います。ビッグデータで溢れる社会において、その大量のデータから意味のある何かを抽出する事が求められています。例えば、あるコンビニで買われる物には、客の年齢、性別、購入物、客が歩いた距離、購入時の天候、季節、周囲にあるライバル店までの距離、近くにあるオフィスビル内の人数、etc...とあらゆる要素が考えられます。ビッグデータとなるとその項目数は物凄い数になります。でも、何となく「そういう項目って沢山あった方がより詳細に知りたい事がわかるんじゃないの?」と思ってしまいがちですが、実は違うんです。項目が沢山あればあるほど「互いに関連を持つ(相関を持つ)項目」や「結果をぼかしてしまう項目」などが増えてしまうんです。これらは知りたい情報を攪乱し、時に間違った答えを導いてしまいます。
ビッグデータから知りたい情報を取り出す式f(x)があるとします。しかし、f(x)はあらゆる項目を含んでいて、項目間の相関や攪乱データによって意図しない答えを出してしまう問題をはらみます。そこで、f(x)に対して例えば「項目数が多過ぎる場合はペナルティーを課す」という「制約」を設けます。すると、式f(x)はその制約上でしか動けなくなります。より少ない項目数になる程ペナルティーは低くなりますが、少なすぎる項目数だと知りたい情報がぼやけてしまう。ここから、程よい項目数(項目の組み合わせ)が導かれてきます。またその程よい項目数の下で知りたい情報を最大化する変数の組み合わせがあるかもしれません。
f(x)という式に対して項目数に対するペナルティーという「制約」…これ、ラグランジュの未定乗数法の考え方の応用です。ラグランジュの未定乗数法は今日のビッグデータ解析と根底の所で実は繋がっていたりします。