2D徴撍曇
偦偺15 懭墌偲捈慄偺嵟抁嫍棧
丂慜復偱懭墌偲揰偺嵟抁嫍棧傪媮傔傑偟偨丅4師曽掱幃傪夝偄偰塢乆偲偄偆戝曄偝偱偟偨丅偱偼懭墌偲捈慄偺嵟抁嫍棧偼偲偄偆偲丄側傫偲偙傟偼揰傛傝傕偢偭偲娙扨偵媮傑傞偺偱偡丅捈慄偺曽偑恾宍偲偟偰揰傛傝傕暋嶨側偺偵偱偡丅娙扨偵側傞棟桼偼乽幨憸乿偵偁傝傑偡丅
嘆 懭墌傪捈慄偵幨憸偡傞
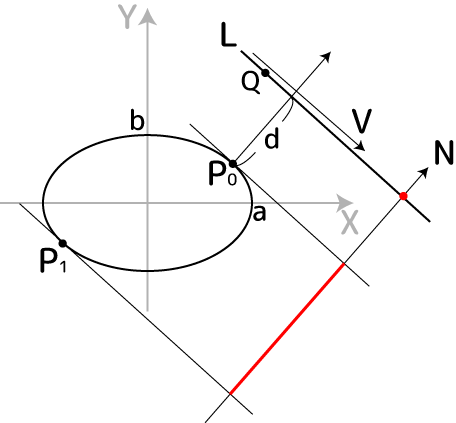
丂崱夞偺峫偊曽傪恾偵偟偰傒傑偟偨丗
丂捈慄L偲懭墌偑偳偺埵棧傟偰偄傞偐抦傝偨偄乮嵟嬤愙揰P0傕抦傝偨偄乯偲偟傑偡丅捈慄L偺曽岦儀僋僩儖V偵悅捈側捈慄傪N偲偟傑偡丅捈慄L傪N偵幨憸偡傞偲丄捈慄偼揰偵側偭偰偟傑偄傑偡乮愒揰乯丅摨條偵懭墌傪捈慄N偵幨憸偡傞偲丄愒偄捈慄偵側傝傑偡丅恾偐傜暘偐傞傛偆偵丄尦偺捈慄偲懭墌偺嵟抁嫍棧d偲愒偄揰偲愒偄捈慄偺嵟抁嫍棧乮抂揰傑偱偺嫍棧乯偼堦弿偱偡丅偱偡偐傜丄幨憸偟偨恾宍偱峫偊傞偲暔惁偔娙扨偵嵟抁嫍棧偑媮傑傝傑偡丅
丂偱偼丄懭墌傪捈慄N偵幨憸偟偨帪偺愒偄慄暘傪媮傔偰傒傑偟傚偆丅偙傟偼巚偭偰偄傞傛傝偢偭偲娙扨偱偡(^-^)丅
丂懭墌偼師偺傛偆偵嬌嵗昗偱昞尰弌棃傑偡丗
揰P偺愙慄儀僋僩儖偼忋偺Px丄Py傪偦傟偧傟旝暘偡傞偲媮傑傝傑偡丗
偙偺愙慄偑幨憸曽岦偵側傞帠偑忋偺恾偐傜傢偐傝傑偡偹丅堦曽捈慄偺曽岦儀僋僩儖V偵悅捈側儀僋僩儖N偼丄V偺X惉暘丄Y惉暘傪擖傟懼偊偰堦曽偺晞崋傪斀揮偡傞偲媮傑傝傑偡丗
偙偺N偲T偼屳偄偵悅捈偱偡偐傜丄偦偺撪愊偼僛儘偵側傝傑偡丗
偙偺兤傪挷愡偡傞偲忋庤偄帠僛儘偵側傞偼偢偱偡丅偦偆偄偆兤偼偲偄偆偲丄師偺傛偆偵揥奐偡傞偲傢偐傝傑偡丗
丂偙偺兤偐傜P0傕偟偔偼P1揰偺嵗昗偑捈愙傢偐傝傑偡丅傕偆堦曽偺揰偼丄愭偺恾偐傜揰懳徾偺埵抲偵偁傞帠偑傢偐傞偺偱兤+兾乧偲偄偆偐P0偺晞崋斀揮偑P1偵側傝傑偡丅揰P0偲P1偑暘傟偽傕偆彑偭偨傕摨慠偱丄屻偼捈慄L忋偺揰Q丄P0丄P1偦傟偧傟傪儀僋僩儖N傊幨憸偟偰廔傢傝偱偡丅
丂捈慄N偼摨偠曽岦傪岦偄偰偄傟偽暿偵偳偙偵偁偭偰傕偐傑偄傑偣傫丅偱偁傟偽揰Q偐傜怢偽偟偰傕栤戣柍偄栿偱偡丅傛偭偰揰Q偼幨憸寁嶼偡傞傑偱傕側偔側傝傑偡丅揰Q傪娷傓捈慄N傊P0丄P1傪幨憸偡傞偵偼埲壓偺幃傪梡偄傑偡丗
丂昗弨壔偟偨儀僋僩儖N偲Q偐傜P0偵怢傃傞儀僋僩儖偺撪愊傪庢傟偽丄Q偐傜N傪偳傟偩偗怢偽偣偽傛偄偐寁嶼弌棃傑偡丅偦傟傪傑偲傔傞偲忋幃偺傛偆偵側傞栿偱偡丅
丂媮傔偨偄嵟抁嫍棧d偼Q-P0傕偟偔偼Q-P1偺嫍棧偑抁偄曽偲側傝傑偡丗
丂d0傕偟偔偼d1偑嵟抁偲傢偐傟偽丄嵟愙嬤揰傕P0傕偟偔偼P1偲婡夿揑偵暘偐傝傑偡丅
嘇 懭墌偲捈慄偺嵟抁嫍棧傪媮傔傞娭悢
丂偱偼懭墌偲捈慄偺嵟抁嫍棧偲嵟愙嬤揰傪媮傔傞娭悢偱偡丗
//
// 懭墌偲捈慄偲偺嫍棧傪嶼弌
// xLen : 懭墌偺X幉曽岦偺挿偝
// yLen : 懭墌偺Y幉曽岦偺挿偝
// x,y : 捈慄忋偺揰偺嵗昗
// vx, vy: 捈慄偺曽岦儀僋僩儖
// dist : 乮弌椡乯嵟抁嫍棧
// px, py: 乮弌椡乯嵟嬤愙揰偺嵗昗
// cx, cy: 乮弌椡乯捈慄忋偺嵟嬤愙揰
bool distEllipseLine( double xLen, double yLen, double x, double y, double vx, double vy, double &dist, double &px, double &py, double &cx, double &cy ) {
double vd = sqrt( vx * vx + vy * vy );
if ( vd == 0.0 ) {
// 捈慄偺曽岦偑掕媊偝傟偰偄側偄
return false;
}
vx = vx / vd;
vy = vy / vd;
double nx = vy;
double ny = -vx;
double th0 = atan2( -vx * yLen, vy * xLen );
double p0x = xLen * cos( th0 );
double p0y = yLen * sin( th0 );
double p1x = -p0x;
double p1y = -p0y;
double t0 = nx * ( p0x - x ) + ny * ( p0y - y );
double t1 = nx * ( p1x - x ) + ny * ( p1y - y );
double r0x = x + t0 * nx;
double r0y = y + t0 * ny;
double r1x = x + t1 * nx;
double r1y = y + t1 * ny;
double d0_2 = ( r0x - x ) * ( r0x - x ) + ( r0y - y ) * ( r0y - y );
double d1_2 = ( r1x - x ) * ( r1x - x ) + ( r1y - y ) * ( r1y - y );
if ( d0_2 < d1_2 ) {
// P'0偑嵟愙嬤揰
dist = sqrt( d0_2 );
px = p0x;
py = p0y;
cx = px + ( x - r0x );
cy = py + ( y - r0y );
}
else {
// P'1偑嵟愙嬤揰
dist = sqrt( d1_2 );
px = p1x;
py = p1y;
cx = px + ( x - r1x );
cy = py + ( y - r1y );
}
return true;
}
丂抁偄(^-^)/
丂揰偲偺帪偲斾傋偰椳偑弌傞傎偳抁偔偰婐偟偔側傝傑偡丅揰偲偺嫍棧媦傃捈慄偲偺嫍棧偑暘偐傞偲僇僾僙儖偲偺徴撍偑庢傟傑偡乮傔傝崬傫偱偄傞帪偵嫍棧傪儅僀僫僗偲偡傞張棟偑昁梫偱偡偑乯丅懭墌傪偦偺傑傑巊偆帠偼偁傫傑傝柍偄偲偼偄偊丄庬椶偑憹偊傞帠偼婐偟偄帠偱偡丅