3D衝突編
その26 レイとカプセルの貫通点
その24でレイと球、そしてその25でレイと円柱との貫通点を計算する方法を見てきました。これらがあると本章のレイとカプセルとの貫通点を検討する事が出来ます。
① カプセルは円柱+半球×2
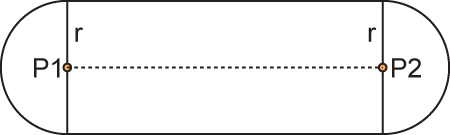
カプセル(Capsule)は線分に一定の厚み(r)を付けた形状をしています。別の例えとして、線分の一方の端点P1を中心点とする半径rの球をもう一方の端点P2に向けてスライドさせた時の軌跡がその形状になります:
図からも分かるように、カプセルは円柱の両端に半球がくっついた形をしています。ですから、このカプセルに向けてレイを飛ばした時の貫通点(衝突点)を求めるには、レイと球、そしてレイと円柱との衝突点が求められれば良いのですが、それらは既に前々章と前章で解説してきました。後はどこから貫通してどこへ抜けるのかを判断できれば良さそうです。
② 貫通パターン
レイがカプセルに当たって貫通するパターンは次の通りです:
パターンは色々ありますが、要は貫通開始点及び終了点が球(半球面)なのかカプセル内の円柱部分なのかを判断できれば良い訳です。その判断をするための図をご覧ください:
球P1、P2そして円柱部それぞれの貫通開始点Q1を求めたとします。もし球P1上にQ1があった場合、∠P2P1Q1が鈍角ならば貫通開始点が球面P1にある事が確定します。「鈍角=内積がマイナス」なので、ベクトルP1P2及びP1Q1の内積がマイナスか否かでその判断が出来ます。同じ事は球P2側でも言えます。
球P1、P2いずれにも貫通開始点Q1が無かった場合、衝突があるとすれば無限円柱のどこかにQ1がある可能性が残ります。もし∠P2P1Q1と∠P1P2Qがいずれも鋭角(=内積がプラス)ならQ1はカプセルの円柱面にある事が確定します。それ以外だった場合、カプセルとレイは交差していません。
ここまでと同じプロセスを貫通終了点Q2についても行います。Q1が存在していればQ2は必ず存在します。
③ 関数公開
カプセルとレイとの貫通点を算出する関数を公開します。関数内で使用しているcalcRaySphere()とcalcRayInfCilinder()は前々章及び前章で公開しています:
レイとカプセルの貫通点を算出 // ∠P1P2P3の内積を算出
// x1, y1, z1: 点P1
// x2, y2, z2: 点P2
// x3, y3, z3: 点P3
float checkDot( float x1, float y1, float z1, float x2, float y2, float z2, float x3, float y3, float z3 ) {
return ( x1 - x2 ) * ( x3 - x2 ) + ( y1 - y2 ) * ( y3 - y2 ) + ( z1 - z2 ) * ( z3 - z2 );
}
// レイとカプセルの貫通点を算出
// lx, ly, lz : レイの始点
// vx, vy, vz : レイの方向ベクトル
// p1x, p1y, p1z: カプセル軸の端点P1
// p2x, p2y, p2z: カプセル軸の端点P2
// r : カプセルの半径
// q1x, q1y, q1z: 貫通開始点(戻り値)
// q2x, q2y, q2z: 貫通終了点(戻り値)
bool calcRayCapsule(
float lx, float ly, float lz,
float vx, float vy, float vz,
float p1x, float p1y, float p1z,
float p2x, float p2y, float p2z,
float r,
float &q1x, float &q1y, float &q1z,
float &q2x, float &q2y, float &q2z
) {
bool Q1inP1 = false;
bool Q1inP2 = false;
bool Q1inCld = false;
// Q1の検査
if (
calcRaySphere( lx, ly, lz, vx, vy, vz, p1x, p1y, p1z, r, q1x, q1y, q1z, q2x, q2y, q2z ) == true &&
checkDot( p2x, p2y, p2z, p1x, p1y, p1z, q1x, q1y, q1z ) <= 0.0f
) {
Q1inP1 = true; // Q1は球面P1上にある
} else if (
calcRaySphere( lx, ly, lz, vx, vy, vz, p2x, p2y, p2z, r, q1x, q1y, q1z, q2x, q2y, q2z ) == true &&
checkDot( p1x, p1y, p1z, p2x, p2y, p2z, q1x, q1y, q1z ) <= 0.0f
) {
Q1inP2 = true; // Q1は球面P2上にある
} else if (
calcRayInfCilinder( lx, ly, lz, vx, vy, vz, p1x, p1y, p1z, p2x, p2y, p2z, r, q1x, q1y, q1z, q2x, q2y, q2z ) == true &&
checkDot( p1x, p1y, p1z, p2x, p2y, p2z, q1x, q1y, q1z ) > 0.0f &&
checkDot( p2x, p2y, p2z, p1x, p1y, p1z, q1x, q1y, q1z ) > 0.0f
) {
Q1inCld = true; // Q1は円柱面にある
} else
return false; // レイは衝突していない
// Q2の検査
float tx, ty, tz; // ダミー
if ( Q1inP1 && checkDot( p2x, p2y, p2z, p1x, p1y, p1z, q2x, q2y, q2z ) <= 0.0f ) {
// Q1、Q2共球P1上にある
return true;
} else if ( Q1inP2 && checkDot( p1x, p1y, p1z, p2x, p2y, p2z, q2x, q2y, q2z ) <= 0.0f ) {
// Q1、Q2共球P2上にある
return true;
} else if (
Q1inCld &&
checkDot( p1x, p1y, p1z, p2x, p2y, p2z, q2x, q2y, q2z ) > 0.0f &&
checkDot( p2x, p2y, p2z, p1x, p1y, p1z, q2x, q2y, q2z ) > 0.0f
) {
// Q1、Q2共球円柱面にある
return true;
} else if (
calcRaySphere( lx, ly, lz, vx, vy, vz, p1x, p1y, p1z, r, tx, ty, tz, q2x, q2y, q2z ) == true &&
checkDot( p2x, p2y, p2z, p1x, p1y, p1z, q2x, q2y, q2z ) <= 0.0f
) {
// Q2は球P1上にある
return true;
} else if (
calcRaySphere( lx, ly, lz, vx, vy, vz, p2x, p2y, p2z, r, tx, ty, tz, q2x, q2y, q2z ) == true &&
checkDot( p1x, p1y, p1z, p2x, p2y, p2z, q2x, q2y, q2z ) <= 0.0f
) {
// Q2は球P2上にある
return true;
}
// Q2が円柱上にある事が確定
calcRayInfCilinder( lx, ly, lz, vx, vy, vz, p1x, p1y, p1z, p2x, p2y, p2z, r, tx, ty, tz, q2x, q2y, q2z );
return true;
}
中々の場合分けになってしまいますねぇ…(-_-;。単純に衝突判定するのではなくて衝突点を算出しようとしているので面倒くさい事になりました。