3D衝突編
その4 線分と板ポリゴン
線分と板ポリゴンとの衝突は、非常に多くの場面で必要になります。飛んでいった矢はどこにいつ刺さるのか?これは、矢を線分と考えて、板ポリゴンとの衝突判定が必要になります。他にはパーティクルに応用が利きます。パーティクルというのはたくさんの点の動きで不定形の物(火花、水、煙など)を表現する手法です。フレーム単位で動くゲームでは点の動きは「短い線分」として表されるので、板ポリゴンに当たったかどうかは重要になります。
① 線分と平面の応用でOK
3D衝突編「その3」で、線分と平面の衝突を説明しました。板ポリゴンは平面の一部ですから、平面との衝突判定を先に行い、ポリゴンとの衝突の可能性がある場合だけに注目した方が簡単です。
ポリゴンに線分が刺さっている状況を想像してみてください。そこには必ず「刺さっている点」がありますね。その点は平面上にあるはずです。つまり、その刺さっている点がポリゴン内にあるかどうかを判定すればよいわけです。ポリゴン内に点があるかどうかは基礎の基礎編「その2」で判定方法を紹介していますので、そちらをご覧下さい。
問題は刺さっている点を確定する作業なんですが、これも良い方法があります。下の図をご覧下さい。
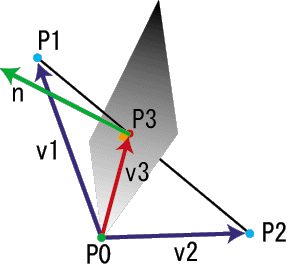
灰色の板が板ポリゴンで、P1とP2間に線分が結ばれています。線分はP3で板ポリゴンに貫通しています。P0はポリゴンの1頂点です。これはどの頂点でもOKです。P0からそれぞれの点にベクトルが伸びています。それぞれv1,v2,v3と名前を付けました。緑色のベクトルはポリゴンの法線ベクトルです。
ところで、みなさん「内分」を覚えていらっしゃるでしょうか?これは高校で習いました。詳しくはこちらをご覧下さい。上の図で内分を説明するなら、次のような式になります。
v3 = (1-a)*v1 + a*v2
求めたいP3はv3があればすぐに算出できます。そのv3はv1とv2と内分比があれば上式から計算できますね。今分からないのはこの内分比です。上の図をポリゴンの真横から見てみましょう。
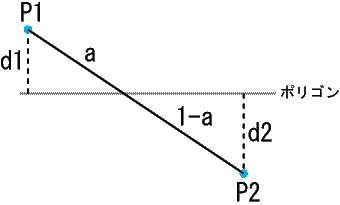
横から見るとこんな感じになっていると思います。ここでd1とd2はそれぞれ点からポリゴンまでの距離です。注目するのは、求めたい内分比が、このポリゴンまでの距離の比と等しいという点です。つまり、
a : 1-a = d1 : d2
ですから、
a = d1 / (d1+d2)
と求めることができます。空間上の点から平面までの距離の求め方は、基礎の基礎編その2「ある点から平面までの距離」ですでに説明してある通りとても簡単に求まります。
長々とした説明だったので、プロセスが複雑に感じるかもしれませんが、やることは次の通り簡単なんです。
① ポリゴンの法線ベクトルと線分の点から平面を貫通しているかどうかをチェック
② ポリゴン平面までの距離から内分比を算出して貫通点の座標を確定
③ ポリゴン内部に貫通点が含まれるかをチェック
①は3D衝突編「その3」で示す判定式1本、②の平面までの距離は一瞬で算出できますし、③もポリゴンの頂点があれば全く問題なくできます。つまり、これによる計算コストは昨今の超速CPUならそれほど大きくは無いのです。具体的な判定の方法は①~③を用いればよいので割愛します(冗長なので(^-^;)