その72 ビュー・射影変換行列が持つ情報を抜き出そう

その72 ビュー・射影変換行列が持つ情報を抜き出そう

　DirectX技術編その39「知っていると便利？ワールド変換行列が持つ情報を抜き出そう」ではワールド変換行列の中からモデルの位置や回転の情報などを抜き出しました。同様に3D描画で必須の行列であるビュー・射影変換行列からもそれらに関連する情報を取り出す事が出来ます。

① ビュー行列からカメラの位置と回転を抜き出す

　ビュー行列は「ワールドに置いたあらゆる物をカメラの世界に移動させる行列」です。そのカメラはDirectXの場合は「原点にあってZ軸方向を向いている」と定義されています。

　本来カメラはワールド空間内にある被写体を取るべく位置と姿勢を持っているというのが日常的な概念ですよね。そういうカメラの姿勢を表す行列は「カメラ行列」と呼びビュー行列と区別されています。

　さて、一例としてワールドの(10, 20, 5)の位置にカメラを置き、Z軸方向を向かせているとしましょう。これを行列で表現すると、

となります。ビュー行列はこのカメラを原点に移動させてZ軸方向を向かせればよいので(-10, -20, -5)だけ平行移動させれば良い訳ですよね。つまり、

です。見て分かるように丁度逆の移動関係にある事が分かりますね。お互いを掛け算するともっと美しい関係がわかります：

そう、カメラ行列とビュー行列はお互いに逆行列の関係にあります。ここからビュー行列の逆行列を求めるとカメラの位置や姿勢の情報が取り出せる事がわかります。ただ、まともに逆行列を計算するのも芸が無いので、カメラ行列の性質を上手く利用して少しスマートにカメラの情報を取り出してみましょう。

　カメラは世界に置かれ、とある方向を向きます。一般にスケールは入りません。これを行列で表現すると、

となります。Rcamは回転行列、Tcamは平行移動行列です。回転してから平行移動するイメージです。この逆行列がビュー行列になります。ところで、掛け算した行列の逆行列には次のような関係があります：

ビュー行列は平行移動行列の逆行列に回転行列の逆行列を掛け算すると求まるという事です。さて、平行移動行列の逆行列は先の例でみたように行列の4行目にある位置情報を反転すれば求まりますね。一方の回転行列は「正規直行系行列」という部類に入る特別な行列です。この部類の行列は逆行列が転置行列で求まってしまうという嬉しい性質があります。ここから、上の式は次のように展開できます：

T(tx, ty, tz)はカメラのワールド空間での位置、そしてX(rxx, rxy, rxz)、Y(ryx, ryy, ryz)、Z(rzx, rzy, rzz)はワールド空間でのカメラの姿勢軸になります。色分けして分かるように、ビュー行列の3行にはカメラの姿勢が転置の形でそのまま収まっています。例えばビュー行列から「ワールド空間でカメラがどの方向を向いているか？」を知るには、青色のZ軸の方向ベクトルをそのまま取り出せば良いだけです。

　一方カメラの位置Tはビュー行列の中の(vx, vy, vz)に計算されて織り込まれてしまっています。位置Tと回転行列の転置行列（＝逆行列）からTv(vx, vy, vz)を求める式を上から抽出するとこんな感じになります：

カメラの位置の反転にカメラの回転行列の逆行列を掛けるとビュー行列の4行目の成分が算出されるという式です。今欲しいのはVt(vx, vy, vz)からT(tx, ty,yz)を求める式です。そこで上式の下2行に注目してみます。これはTとVの関係式になっていますね。この式の右側から元の回転行列を掛け算するとこうなります：

ビュー行列の4行目の値に元のカメラの回転行列を掛けると、カメラの位置の反転が得られる事がわかりました。元のカメラの回転行列はビュー行列の3行に転置した形で収まっているのでした。つまり、上式の右辺は元のビュー行列内の成分だけから計算が可能であるわけです。すなわち、

となります。ビュー行列内の成分で上の式を表現し直すとこうなります：

わーお、結局は「ビュー行列の4行目に対して1行目、2行目そして3行目の内積を取って符号反転すると元のカメラの位置が求まる」という綺麗な式になりました！

② 射影変換行列から近平面距離、遠平面距離、視野角、アスペクト比を取り出す

　続いて射影変換行列の中のパースペクティブ行列から近平面の距離（Zn：Z near）や遠平面までの距離（Zf：Z far）、視野角（fovY）そしてアスペクト比（Ar：Aspect ratio）を取り出してみます。

　まず次の典型的なパースペクティブ行列を仮定します：

D3DXMatrixPerspectiveFovLH関数が返す行列はこれです。WとHは画面の幅と高さ（ピクセル）、θは視野角（fovY）です。

　まず簡単なのは視野角θ。m22成分から、

とアークタンジェントを使って逆算で求まります。

　画面のアスペクト比は As = [画面幅W]/[画面高H] で定義されます。これはm11成分とm22成分を使えば簡単に求まります：

　次はZnです。m33とm43成分を良く見ると、m43成分はm33成分に-Znを掛けただけなのが分かります。この関係式からZnを導きます：

簡単(^-^)。

　Znが計算出来ればZfはm33からこちらも簡単に求まります：

③ 付録：ビュー行列、パースペクティブ行列、ビューポート行列の逆行列の式

　情報を抜き出すという事では無いのですが、パースペクティブ行列とビューポート行列の逆行列の式を掲載します。これらの逆行列はスクリーン座標からワールド座標やローカル座標などを逆算する時などに利用できます。左側が元の行列、右側がその逆行列の式です(^-^)。
横に長くてすみません(^-^;;

　Rcam,x：　ワールド空間でのカメラの姿勢X軸
　Rcam,y：　ワールド空間でのカメラの姿勢Y軸
　Rcam,y：　ワールド空間でのカメラの姿勢Z軸
　Tcam：　ワールド空間でのカメラの位置座標
　W,H：　画面の幅と高さ（ピクセル）
　θ：　視野角（fovY）
　Zn,Zf：　近平面及び遠平面までの距離

	行列	逆行列	逆行列（元の行列の成分で作る）
ビュー行列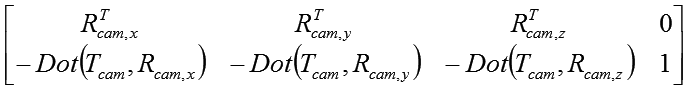
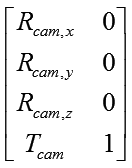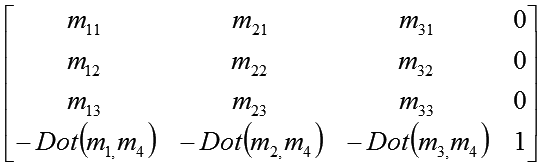パースペクティブ行列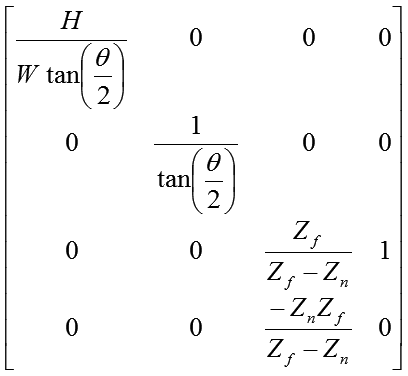
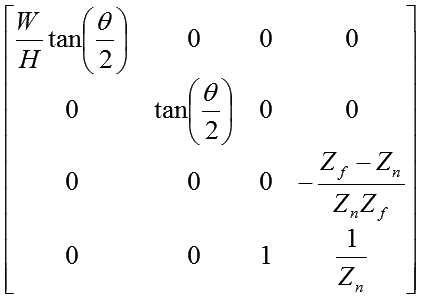ビューポート行列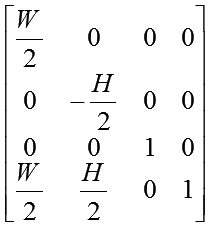

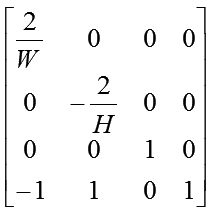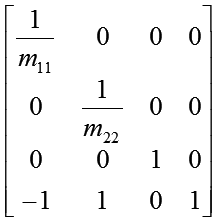　こう見ると、主要行列の逆行列は元の行列やその行列を作るのに必要なパラメータから簡単に得られるのが分かります。