
ホーム < ゲームつくろー! < プログラマブルシェーダ編
シェーダ編
その7 斜めから見ると底が見えない水面(フレネル反射)
前章で環境マップについて説明しました。環境マップを使うとモデルの表面に背景が反射して金属のようにテッカテカになります。実装も簡単で効果が非常に高い楽しいシェーダです。
さて、背景を反射させるものは何も金属ばかりではありません。ガラスの表面や水面など、表面がツルッとしているものは大抵背景を反射します。逆に言うと私たちは「ツルッとしている」というのを背景が映り込んでいる事で認識しているわけです。
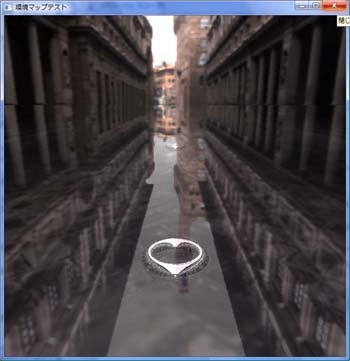
では波が一切たっていないそれこそガラスのような水面に環境マップを適用するとどうなるでしょうか?ちょっとテスト画面を御覧下さい。
縦に並ぶトーラスはいずれもy=-100.0fの位置に沈んでいて、水面はy=0.0fに広がっています。水面自体は単なる平面ポリゴンで、その表面に環境マップを適用しています。水面ポリゴンのα値は0.20fでわずかに背景を反射しています。
上の絵に違和感を覚えるのは、遠くのトーラスまでくっきりと見えているためです。実際の水面はそうなりません。そこで下の写真を御覧下さい:
下の写真を御覧下さい:
この実験をしたのは午前4時…マルペケがんばってます(T-T)g
これは水面に映る「絵」がどうなるかを実際に実験してみたものです。深皿に青色に色を付けた水を張り、かなり斜めの角度から撮影しました。わかりにくいのですが、実は水底に10円玉を一列に沈めています。
これを見ると、水面というのは遠くに行くほど背景を良く反射しているのがわかります。手前側は水の色が見えますが、奥は後ろの扉の白い色やワインのビンがより濃くでていますよね。また少しわかりにくいのですが奥の10円玉ほどぼやけて見えなくなっています。もっと奥行きのある水面であれば、これらの現象はさらに顕著になります。遠くに行くほど背景を映し出し、手前ほど底が見える。そういう微妙なグラデーションを見て私たちは「これは水だ」、もう少し拡張していうなら「半透明のつるつるとした表面だ」と認識しているんです。
この自然現象を冒頭のモデル描画に反映して水面を表現するにはどうしたら良いのか?それを紐解くのが「フレネル反射」です。
① フレネル反射
フレネル反射(Fresnel Reflection)とは、正に先程の水面に見られる現象を表す反射です。Wikipediaはこちら。フランスのオーギュスタン・ジャン・フレネルさんが提唱しました。
フレネルさんはこう考えました。「透過する平らな物に光が鉛直に近い角度で飛び込んだら、その光の大部分は透過物を貫くだろう。一方で平行に近い角度で飛び込むと、水面で反射してしまい光は透過物内にほとんど入らないだろう」:
そして、物の透過度や光の強さなど色々な要素から光がどのくらい透過物の表面を反射し、どの位が透過物の内部に入るかを計算する式を作りました。それが「フレネルの式(Fresnel Equations)」です:
ここでRは反射率、αは入射光の入射角度、βは屈折光の法線との屈折角度です。
○ 上記フレネルの式に関して(2019.7追記)
上のフレネルの式ですが、元式を掲載した2010年当時確かWikipediaにあった気がしたのですが、現在(2019.7)は見当たりません。よって現在出典元不明になっています。式の形と現在のWikipediaの説明から類推するに、sin側の2乗式は「s波」のエネルギーの反射率、tan側は「p波」のエネルギーの反射率になっています。それを足して2で割っているという事は、双方のエネルギー反射率の平均値を取っている事になります。出典が不明になってしまった現時点でこの式の厳密性は保証できないのでご注意ください。もしこの式が載っているサイトや書籍がありましたら是非教えて下さい m(_ _)m
反射率が100%ならば背景が全部映るのですから、それは不透明な金属のような物になります。一方で反射率が0%なら、水面の下の物が完全に見えます(要は空気と同じ)。つまり、反射率は水面ポリゴンのα値そのものというわけです。
上の式で、入射角度αは視線と法線の作る角度なので既知です。一方で透明物の中に潜り込んだ光と法線とが作る屈折角度βはどうしたもんでしょうか?実は、この角度は入射光が進んできた物(上の場合は空気)そして飛び込んだ物(水)それぞれの「屈折率」があると「スネルの法則」という法則から求めることができます。スネルの法則は次のようになっています:
n1は入射光が進んでいる物質の屈折率、n2は透過物の屈折率です。非常に単純な法則ですね。物の屈折率は物特有ですでに知られていますので、上の式から、
とsinβが求まります。もちろん、ここからβを求めるのは簡単です。それよりも、上の式はフレネル反射を計算するときに「入射角度だけあれば良い」事を示しています。これは凄い嬉しい性質なんです。
ただ、そうは言ってもまだtan(α+β)など角度を足し算したtanなどを求めなくては行けません。もう少し何とかしたいところです。
三角関数(sin, cos, tan)はお互いに密接に関わり合っています。ごにょごにょすると相互に変換できたりします。tanもsinで表すことは一応可能です。では何を基準にしたら良いか?実は、今私たちが得ることができる最も簡単な値は「cosα」です。なぜなら、入射ベクトルと法線ベクトルはどちらもシェーダ内で簡単に手に入る情報で、これらがあると、
と2つのベクトルの内積で計算出来ます。cosαがあればsinαも算出出きて、sinαがあればスネルの法則からsinβも出せて…と、フレネルの式にある三角関数はとことんcosαで表せるようになります。で、うらーーーっと頑張ると次のような式になります:
A,B,Cそれぞれを先に算出しておけば、反射率Rは上のように単純な数値式で計算できます。Cは実際AとBだけで構成されているので、実質はA(屈折率比)とB(入射ベクトルと法線の内積)だけでフレネル反射は計算ができるわけです(^-^)。これなら、シェーダ内でも何とかなりそうです。
② フレネル反射の適用
では実際にフレネル反射を冒頭の絵を作ったシェーダに適用してみます:
| フレネル反射適用 | 適用前 |
 |
 |
適用後は遠くにあるトーラスがうっすらと見えるくらいになり、また遠くの景色が非常に強く反射しているのがわかります。右の適用前の絵にある違和感はありません。
ピクセルシェーダの実装を見てみましょう:
// 環境マップ用ピクセルシェーダ
const char *pixelShaderStr =
textureCUBE cubeTex;
float refractiveRatio : register(c0);
samplerCUBE cubeTexSampler =
sampler_state {
Texture = <cubeTex>;
};
struct VS_OUT {
float3 normalW: TEXCOORD0;
float3 viewVecW: TEXCOORD1;
};
float4 main( VS_OUT In ) : COLOR {
// フレネル反射率計算
float A = refractiveRatio;
float B = dot(-normalize(In.viewVecW), normalize(In.normalW));
float C = sqrt(1.0f - A*A * (1-B*B));
float Rs = (A*B-C) * (A*B-C) / ((A*B+C) * (A*B+C));
float Rp = (A*C-B) * (A*C-B) / ((A*C+B) * (A*C+B));
float alpha = (Rs + Rp) / 2.0f;
float3 vReflect = reflect( normalize(In.viewVecW), normalize(In.normalW) );
float4 color = texCUBE(cubeTexSampler, vReflect);
color.a = min( alpha + 0.20f, 1.0f);
return color;
} ;
フレネル反射率の計算は、①の最後に示したうらーーーっと展開した式を素直に使っています。最終的に透過度であるalphaを求め、環境マップが拾ってきた色のα値として適用しています。上のフレネル反射率の計算部分は関数化してしまっても良いですね。
環境マップとフレネル反射が入ることで、物の質感は相当に良くなります。実装もそれほど難しくありませんし、うまく使っていきたいですね。