VisualStudio + Pythonでディープラーニング
ドロップアウトでふわっとフィッティング
(2019. 12. 20)
前章で過学習のヤバさを色々と説明してみました。過学習を起こしたモデルは本番の入力値に対して誤差混じりの推定値を返してしまう可能性が高くなります。それを防ぐには過学習を回避しなければなりません。その回避方法の一つとして有効なのがドロップアウトです。
ドロップアウトは学習時に層から出力される値をわざとゼロと無効化する事で情報を疎な状態にしぼんやりさせる事で極端な値や外れ値の影響を軽減させる方法です。これにより学習データにバッキバキにフィッティングしてしまう過学習を防ぎます。その分評価関数の値は大きくなりますが、少なくとも過学習してしまったモデルよりは真のモデルに近しい形状になる事が期待されます。ここではそんなドロップアウトをKerasで設定して実際にその効果を体験してみましょう。
① Kerasでドロップアウトを設定
Kerasではドロップアウトはそうと層の間にフィルタとして設定します。設定方法は非常に簡単で以下のようにします:
import keras
import numpy
#モデル作成
model = keras.Sequential()
#ドロップアウトを第1層と第2層の間に設置
model.add( keras.layers.Dense( units=5, input_shape=(1,) ) )
model.add( keras.layers.Dropout( rate=0.3 ))
model.add( keras.layers.Dense( units=1 ))
model.summary()
ドロップアウトはkeras.layers.Dropoutクラスが担います。引数にあるrateはドロップアウト率というもので、前の層の出力の内何割をゼロに置き換えるか指定します。上の設定だと30%の出力値がランダムにゼロに置き換わります。
② ドロップアウトの効果を実験してみよう
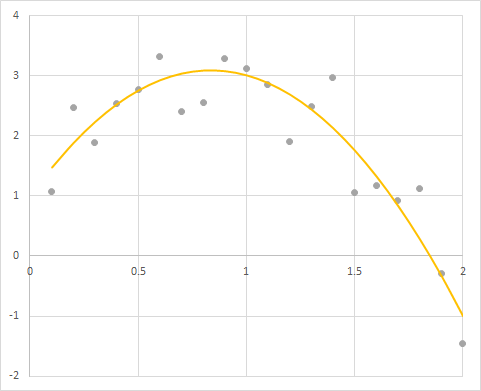
ではドロップアウトがモデル推定にどういう効果をもたらすか実験してみましょう。目で確認できるデータとモデルの方が良いので、次のような放物線に誤差を含ませたデータを使う事にします:
データ点は20個あります。上に凸な非線形の分布をしているので、ReLUを活性化関数に使って頑張ってフィットしてもらいましょう。モデルの構成は以下のようにしてみます:
第1層のニューロン数は豪華に100個う事にします。1層目と2層目の間にDropout層を挟みます。毎回25%のデータをランダムにゼロに置換して第2層へ渡します。第2層は単純に足して欲しいのでLinearにしています。最終的な出力は1次元なのでニューロン数も一つです。
この構成をそのままKerasのコードにすると次のようになります:
import keras
import numpy
#モデル作成
model = keras.Sequential()
#ドロップアウトを第1層と第2層の間に設置
model.add( keras.layers.Dense( units=100, activation="relu", input_shape=(1,) ) )
model.add( keras.layers.Dropout( rate=0.25 ))
model.add( keras.layers.Dense( units=1 ))
#確率的勾配降下法で検索、平均二乗誤差で評価
sgd = keras.optimizers.SGD( learning_rate=0.05 )
model.compile( optimizer=sgd, loss='mse' )
model.summary()
#学習データ
trains = numpy.array([
[0.1, 1.07465136169627],
[0.2, 2.46096169578079],
[0.3, 1.89292513452307],
[0.4, 2.54202552072304],
[0.5, 2.7676741381971],
[0.6, 3.31525260648683],
[0.7, 2.39599389495914],
[0.8, 2.54978601081886],
[0.9, 3.28575296659775],
[1, 3.1149829165523],
[1.1, 2.85086983463959],
[1.2, 1.9015258225872],
[1.3, 2.47732784273557],
[1.4, 2.96141087282737],
[1.5, 1.06197633999513],
[1.6, 1.1740911923245],
[1.7, 0.916128014777561],
[1.8, 1.1224218544772],
[1.9,-0.300700142423865],
[2, -1.4551134452423]])
train_x = trains[:, 0:1]
train_y = trains[:, 1:2]
#学習開始
model.fit( train_x, train_y, epochs=1000 )
#モデルによる推定値を出力
test_x = numpy.arange( 0.1, 2.0, 0.05 )
estimate = model.predict( test_x )
print( estimate )
毎度思いますがシンプルな構成だとKerasはホント短く書けて良いですね(^-^)
この実験コードと一緒にrateを0、つまりドロップアウトの効果を無くしたコードを走らせ、それぞれについてモデルから推定された値をプロットしたのが下のグラフです:
黄色いグラフが真の2次関数、点は誤差を含めて作成したデータ点です。赤いグラフがドロップアウト(rate=0.25)による推定値、そして青いグラフがドロップアウト無しの推定値です。
青いグラフは見た目ですがデータ点の動きに良く合っています。ただ頑張って合わせているためかx=1辺りでカクンと折れ曲がっていますね。またその折れる箇所の左右では直線的になっているのも見て取れます。過学習が進んでデータに依存した形状と言えるかもしれません。
一方ドロップアウト層を挟んだ赤いグラフは、青いグラフよりも柔らかいフィッティングになっていますよね。データ点の凸具合よりは平坦的ですが、全体的に過不足ないフィッティング具合に感じます。もし黄色い理論線と一番左端の点が無かったとしたら、人の目で見ても赤い方のグラフに近い近似線を書くのではないでしょうか。このようにドロップアウトを入れるとフィッティングが柔らかく、誤差に鈍感なモデルになります。
③ ドロップアウト率はどの位が適正か?
ドロップアウト層にはドロップアウト率を設定する必要があります。これは0~1まで好きな値を入れて良い訳ですが、どの位が良い塩梅なのでしょうか?もちろんこれはケースバイケースかもしれませんが、上の実験で率を変えて試してみました。その結果がこちら:
一番尖っているのがドロップアウト無しのグラフで、そこから下方向へ徐々に柔らかくなっているのがわかります。これを見ると50%でもそれなりなフィッティングをしているように見受けられます。バランスが良いのはやっぱり0.25位のかなと思いますよね。ですから、ざっくりですがドロップアウト率は0.2~0.4位が適正のようです。
という事で、この章ではドロップアウトの効果を実験してみました。こんなに明確に効果が出るのですからお得ですね。少なくともニューロン数が多い層については過学習の影響を避けるためドロップアウトを入れた方が無難に感じました。