その4 波:平面を直進するsin波を作る
波と言えば三角関数です。周期を与えるだけで-1~1の間で周期してくれる三角関数は、波を作るための豊かな性質を沢山持っています。この章ではsin関数を使って平面の特定方向へ流れる周期性のある波を発生させてみます。
① sin波を作る
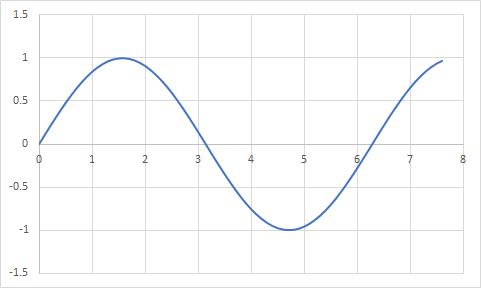
sin関数と言えば言わずもがな次のような周期性をもった関数です:
0~2πで1周期、その間に高さHは-1~1まで変化します。これを色々加工して好きな波を作ります。まず簡単な所で「振幅(Amplitude)」、つまりグラフの縦幅を変更するには右辺に係数Aを掛け算するだけです:
A=5の場合を青色のグラフで示しました。縦軸のスケールが変わっている事に注意です。元のsin(x)はオレンジのグラフです。周期は変わりませんが振幅は大きくなっていますよね。一つ言葉上の注意点として、「振幅」というのは波の高さの中心から波頂までの高さまでを言います。上のA=5だと高さの中心は0ですから振幅5となります。一方「波高」というと波の一番底から波頂までの高さを指します。A=5の振幅である青い波は、高さ10の波高である訳です。本章以降では基本振幅を使用していきますが、場合により波高も出てくるきますのでご注意ください。
次は「波長(Wave length)」を変えてみます。波長とは波の高い所から次の高い所までの距離です。波長を長くするにはxの値がなるべくゆっくり進行するようにすれば良いわけです。つまりx=x/Lとすれば、波長が長くなる程xの増加量が緩やかになります:
A=1、L=0.5、波長が半分の場合を描いています。オレンジのデフォルトsin(x)が1周する間に2回うねってますよね。振幅と波長はお互いに干渉せずに作用するので、同じ波長で振幅が2倍の波を作る事も簡単です。ただ、上の関数定義だと波長Lの定義通りにはなっていません。だって、上の青グラフの波長は3.1415...つまりπになっていてL=0.5ではありません。これはxが周期変数だからです。L=0.5と関数に入れた時に結果もその通りになるようにするには、波長Lを1周期である2πで割り算しないといけないんです:
これでばっちりです(^-^)。そしてこれによってxが「位置座標」もしくは「ある地点からの距離」という位置付けになりました。上の青いグラフでx=0.5m地点の波の高さは0です。
ここまでで、振幅Aと波長Lを定めれば、ある地点xでの波の高さを求める事が出来るようになりました。でも、波は動いてなんぼです。一般に水面の波は水平方向に「ズレ動く」ように見えます。ただ実際には波を構成している水が横方向に動いているのではなくて、水の高さが時間と共に変化していて、その結果ズレ動いているように感じられているだけです。
とはいえ、波の高さは平行にすーっとスライドしていく事には変わりません。平行にすーっと動く事を「位相(Phase)」と言います。上のsin波をプラス方向へ位相させるには、位置であるxに位相分の値を「引き算」すると上手くいきます:
青色がP=0で、オレンジ(P=0.05)、灰色(P=0.1)とプラス方向に波が移動しています。この時各地点xの高さの変化はPの変化が一定速度ならちゃんとsin波になります。これで波を表現する3つの要素「振幅」「波長」「位相」が揃いました(^-^)。
② 自然の波の振幅と位相速度
ところで、上の図からもわかるのですが、例えば位相速度がすっごく遅いとすると、見た目波はその場で氷固まったかのように動いていないように見えます。液体の水でそんな事は無いですよね。また、例えば津波などは時速100km以上という猛スピードで移動する事が知られていますが、お風呂に入った時の水面の波がそんな速度で動いている訳もありません。さらに言えば、上のグラフのように波長が50cmの波で波高が2mもあるような比率の波は自然の波としてはあまりに不自然です。ただ、波長に関しては、自然にはごくごく短い波長の波から数百mになる物まであらゆる波長の波が実際発生しています。どうやら波長は自由度がありそうです。
このように、数学としてのsin波はいくらでも形を変えられますが、自然の波は波長に対する波高(振幅)及び位相速度がある程度決まっています。
〇 波長と振幅の関係
波長Lと波高については、モデル研究やシミュレーション、実際の波の測定などから、波長を1とした時の最大波高がおよそ1/7(0.142)程度である事が知られています(こちらのサイトなど参考)。波長が10mの波ならば波高は精々1.4m以下であるという事です。これ以上高くなると波は自然と崩れてしまいます。海岸付近で波が崩れるのは、浅い所に伝わってきた波の波長が変化し(浅くなる程波長は短くなる)、波高との比率が1/7を超えてしまうために起こります。
①で度々挙げていた波長Lが0.5(50cm)の波について、振幅Aを50cm×(1/7)/2 = 3.5cm (振幅は波高の2分の1なので2で割っています)程度にすると下のようなグラフになります:
L=0.5、A=0.0357、P=0の波
確かに自然の波ってこのくらいかなぁという感覚がありますよね。もちろん凪(なぎ)の時は振幅はもっと小さくなります。一般に天候が荒れるとどの波長の波でも波高は大きくなり、穏やかだと波高も低くなります。完全にフラットの時を0、最大にヤバい時を1とする「波やべぇパラメータQ」を設定するとしたら、波長と振幅の間に、
という経験則的な計算式を持ち出しても良いかもしれません。これなら波長を与えれば波やべぇ度Qに合わせた振幅が計算されるので波ごとに都度振幅を与える必要が無くなります。
〇 波長と位相速度の関係
位相速度が0の大波はもはや固体です(^-^;。波の速度が時速100kmあるお風呂もありません。このように、波長と位相速度には何か関係があります。これには重力が関わっています。波長に対して水深が十分に深い条件で、波の速度vと、波長L、そして重力加速度gには以下の関係がある事が知られています:
例えば波長10mの中々な大波の場合、
およそ秒速4m進むようです。これは時速にすると約14km。小走り位の速さです。別例として、津波は高さ15mなどとなります。波高の7倍程度が波長なので、この津波の波長は約100m。上の式に入れると秒速12.5m/s。丁度25mプールを2秒で走り抜ける程のスピードです(水深が十分に深い場合)。恐ろしい…。
という事で、波長に対する振幅及び位相速度の関係がわかったので、これを①の最後の式に代入すると、次のような波長Lと経過秒tそして波やべぇ係数Q(0~1)で決まる自然の波の方程式が出来上がります:
③ 平面でのsin波:環状波
さて、ここまでの位置情報は1次元、つまり位置xのみが存在する世界でした(縦軸Hは波の高さなので地理的なポジションではない)。これに対し水面はXとYの2次元平面です。あるX座標とY座標、そして時刻tを与えると高さHの値が一つ出てくる、これは次のような2+1変数関数である事を意味します:
関数の中に位置xとy、そして時刻tが一緒に含まれているという事です。これを念頭に置いて平面でのsin波を考えてみましょう。
例えば池に小石を投げ入れたり、水を張ったお風呂に水滴が一滴ポチャンと落ちた時、そこを中心として波紋が円形状に広がります。これは中心点からの距離に対応した波が発生したためです。同じ距離dであればその地点の波の高さは同じになるとすれば、変数がd一つだけになるので、②のsin波をそのまま適用できます。水滴の落ちた位置を(x0, y0)とすると、ある地点(x, y)での波の高さは:
となります。
この環状波を使って実際にハイトマップを描いてみるとこんな感じになります:
正方形の領域の一辺は1mで中心が(0,0)です。左が波長L=0.5mで(-0.5,0)から環状波を発生させた場合、右が波長L=0.25mで左下から発生させた場合です。同心円状に広がる波紋ぽい高低差になっていますよね。(波の高さはノーマライズしています)
③ 平面でのsin波:直進波
環状波は凄く小さなスケールでの波で良く見られますが、海面のようなマクロの波の場合、少なくとも環状に大きく広がっているようには見えません。これは一つには波の発生源が物凄く遠くにあって、目に見える所に届いた頃にはその半径が巨大になり、殆ど真っすぐの波しか見えなくなっている為です。そういう波で小さな物はエネルギーが無くなって目に見える頃にはほぼ見えなくなってしまいます。もしくは色々な波が混ざり合う中でその特徴が消えてしまいます。よって、そういう直進する波の多くはエネルギーをたっぷり持った大きな波です。
状況はさて置き、海のようなマクロな領域の大きな波を表現するには、環状波ではなくある一定方向に並走して動く波(直進波)が必要になります。
直進波が動く方向を「風の向き(Brow)」Bと表すとします。同じ高さの座標を結ぶと下図のように向きBに直行する直線状に見えます:
ここで原点を通る直線(同じ高さの座標点の集まり)を起点と考える事にします。直進波なのでこの起点直線からBの方向に距離dだけ進んだ地点の波の高さはすべて一緒です。ここから直進波を作るには距離dが求められれば良い事になります:
上図の距離dは内積の性質「単位ベクトルと任意のベクトルとの内積は、その単位ベクトルに任意ベクトルを投影した時の長さになる」から、方向ベクトルB(単位ベクトル化します)と(x,y)の内積で簡単に求まってしまいます:
これを②の環状波の時と同じようにsin波のdの所に代入すると、
という直進波の式が出来上がります。時刻tを進めると風の向きBの方向に直線的な波がす~っと進んでいきます。こちらも実際ハイトマップを作成してみると、
こんな感じになります。
この章で作成した環状波と直進波は一定周期で無限に続くsin波です。ハイトマップを見て感じる通り、1つの波だけだと非常に機械的な波に見えます。これを自然の波に近い見た目にするには「波の合成」が必要です。これについては後の章で説明しますが、先に波の表現として外せない大切な性質「波頭が尖る」という事について次の章で見ていく事にしましょう。