ソフトウェア編
その5 ステージの指定の位置に移動させるには?
現段階で、時間を指定するとボタンを押したり離したり出来るようにはなりました。しかし、この指定は手作業で行うにあまりに異常な作業です。例えば、次のような位置の移動を考えて見ましょう。
テクニクビートのステージの一部分だと思ってください。斜め45度や縦横などの移動は簡単です。テクニクビートは8方向レバー対応なので、レバーを入れっぱなしにすればよいわけですから。しかし、それ以外の角度へ移動するためには、方向キーを入れたり戻したりと微妙な調整を要します。人が操作する場合は無意識に調節しているんですが、機械にとって、それは大変に難しい作業なのです。
この章では、キャラクタをステージの指定の位置に移動させるための方法について検討し、どういったアプリケーションを作成すると自動移動の設定が楽にできるのかを最終的に考えてみます。
① 最短の経路とは?
ある位置から8方向レバーだけで指定の位置に行くには、どういう経路を通ればよいのでしょうか。この答えは沢山あるのです。一番簡単なのは「直行移動」でしょう。
これも決して悪くありませんし、何より簡単です。ただ、この移動は移動距離が長くなってしまいます。簡単な曲ならばこれで十分ですが、高レベルの曲になると、これではとても間に合いません。次のように少し分けるのはどうでしょう?
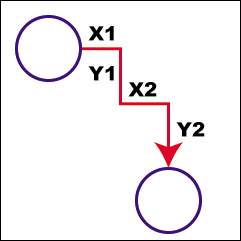
これは実質先ほどと時間が変わりません。X1+X2=Xですから距離が同じなんです。つまり、4方向だけで考えると、どういう風にレバーを入れてもある位置に移動する距離も時間も同じになります。
一方8方向レバーでは45度方向に移動することが可能です。これで任意の位置となると、ちょっと複雑そうな気もしますが、実は簡単な法則に収束します。斜め方向を加えた時の移動方法は次のようになります。
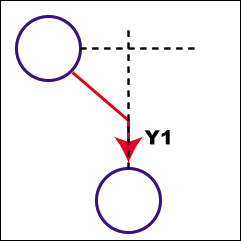
最初に斜めに進み、縦軸がそろったところで後は直行に移動すれば、指定の位置に移動できます。実は、これが8方向レバーでの最短経路になります。よって、今後はこの移動方法で統一します。
② キャラクタの速度をどうするか?
移動の方法はわかりました。しかし、まだまだ大変です。テクニクビートのキャラクタは、それぞれ移動速度が異なります。しかも、キャラクタによってはアクションを起こしている時や消した後に移動速度が変化します。こうなると、単純には特定の位置に移動できなくなります。まずは、各キャラクタごとの移動速度の特徴をまとめてみました。
| Willie | Cart | Hassy | Knitty | Rain | Bot | |
| 通常移動 | 遅い | 速い | 遅い | 普通 | 普通 | 普通 |
| 反応時 | - | - | - | - | 速くなる | - |
| アクション時 | 速くなる | 硬化時間あり | 速いが制御不能 | - | 遅くなる | 高速 |
これをみると、大変にありがたいキャラクタがいます。「Knitty」です。移動速度は普通ですが、何をしても速度が変わりません。使用するキャラクタをKnittyにする事で、速度の問題を回避できます。「ARIKAさん、ありがとう」と感謝感謝です。ただ、もしかしたらKnittyで完璧クリアが出来ないステージがあるかもしれません。その時は、また対策を考えましょう。
指定の場所に行くためには、Knittyの速度を知る必要があります。こればかりは実際に動作テストをして決めるしかないでしょう。しかし、速度が分からなくても、相対的な位置の指定は出来ます。キャラクタの速度を1単位と考えれば、遅いWillieでも速いCartでも1Flip辺りで単位距離進むことに変わりはありません。ですから、輪の出る位置を指定すれば、とりあえず相対的な移動時間を算出できます(細かなことはそのうち示します)。
③ そういえば、テクニクビートは斜め視点ですが・・・
指定の場所に行く方法が確定しました。ところで、テクニクビートのは斜め3D視点です。位置を指定するのが大変そうに思えます。しかし、これはまったく問題がないんです。それは、ステージは斜め視点ですが、移動方向は方向キーの通りだからです。つまり、こういうことです。
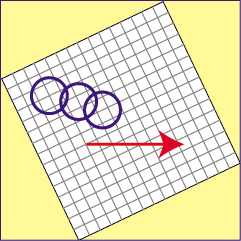
内側の正方形がゲームで使用されているステージで、実際傾いています。しかし方向キーは矢印のように外側の正方形にあわせる方向となります。輪の出る位置を外側の正方形の座標と考えてしまえば、ステージがどう傾いていても問題ないわけです。
④ 次の位置までの方向キー押し下げ時間の自動計算
ここからはちょっと面倒な計算の話になります。ある位置にいるKnittyが次の位置に行くまでに、どの方向キーをどれくらい押し下げるかを計算してみましょう。まずは座標をご覧ください。
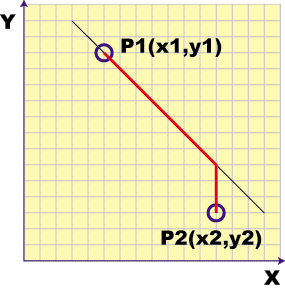
キャラクタはP1の位置にいて、次にP2の位置に移動したいとしましょう。升目の数を単純に数えてみます。まず右下に7マス分入れて、右を離し、さらに3マス分下に入れ続けます。これを成分で分けると、右7マス分、下10マス分キーが入っていることがわかります。これをタイムスケールに直してみましょう。
実はこれは間違い・・・
行きたい方向の縦横のマス数を数えてその長さだけボタンを押せばよいかのように感じます。ところが、これではダメなんです。というのは、「斜めに移動すると縦横成分方向の速度が落ちる」からです。斜めに移動している間、縦横成分の移動量は通常時の0.707倍になります(これはルート2の逆数です)。よって、横7マス分を斜めに移動するには、
7マス * ルート2(1.414...) = 9.898マス
だけボタンを入れる必要があるのです。正しくは次のようになります。
.gif)
まとめると、ボタンを押す時間は次のように計算されます。
| ① 縦横で成分(絶対値)が小さい方の距離Dminを計算 ② Dmin * 1.414の距離を進むのに必要な時間Tcrossを算出(Knittyiの速度が分かれば可能) ③ 成分の絶対値の差分Ddefを算出 ④ 差分を進むのに必要な時間Tdefを算出 ⑤ 絶対値が小さい方の押し下げ時間はTcross、大きい方の時間はTcross + Tdef |
この移動アルゴリズムに従えば、最短経路を常にたどって行けます。
⑤ アプリケーションの見た目
以上から移動を定義するアプリケーションのGUIのイメージは次のようになるでしょうか。
こういうらしいスケッチが描けるIllustrator(Adobe)は偉大です
・・・これはちょっと、やりすぎかもしれません(^-^;。ま、ここまでとは行かないまでも、これになるべく近づけてみようかとは思います。