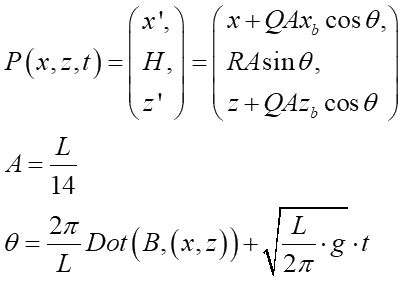
※Bは波の移動方向ベクトル、Rは波の高さの調整項(通称波やべー係数)
その10 波:ゲルストナー波を合成する
前章で平面プレートの頂点の高さを頂点シェーダ内で直接計算してゲルストナー波を起こしてみました。ある方向へうねらす直進波はこれで十分です。ただ、波が正確にある方向にだけ直進するのは不自然さがあります。自然の波は様々な波が折り重なって形成されています。大波であるゲルストナー波も色々な方向から折り重ねる事でより自然になります。
① 波の合成は単純な足し算、ただしベクトルとして
波の合成とは高さの足し算です。これは水の波も音の波も一緒です。要は全ての波の値を単純に足せば良いと。そこで前章のゲルストナー波の式を再掲します:
※Bは波の移動方向ベクトル、Rは波の高さの調整項(通称波やべー係数)
式の意味や各パラメータの詳細は前出の章に譲るとしまして、Pが波となる頂点の位置と見て下さい。波の高さP.yについては単純な足し算で良いのですが、ゲルストナー波は元の頂点水平位置(x,z)が(x', z')にスライド移動します。よってこのスライドのベクトルを足さないとおかしなことになります。それを踏まえて複数のゲルストナー波の合成式を書くとこうなります:
完全に平坦な時の位置(x,0,z)に水平方向ベクトル(x,z)及び高さyをすべて足し合わせています。シグマの中身はこれ以上綺麗になる物では無いのでまぁガシガシ足していきましょう(^-^;
② 法線は正規化して足し算、合成法線も正規化で
法線は元からベクトルなので位置よりは単純で、そのまま足し合わせてOKです。ただし各ゲルストナー波ごとに法線は正規化しなければなりません。そして全部足し合わせた後の法線も正規化が必要です:
これも特に綺麗に出来る類では無いのでそのまま足し合わせてしまいましょう。
③ ゲルストナー波合成シェーダ
上記を踏まえたシェーダを書いてみます:
Shader "IKD/GerstnerWave"
{
Properties
{
_MainTex ("Texture", 2D) = "white" {}
_BaseColor ("Base color", Color ) = (1.0, 1.0, 1.0, 1.0 )
}
SubShader
{
Tags {
"RenderType"="Opaque"
"LightMode"="ForwardBase"
}
LOD 100
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
// make fog work
#pragma multi_compile_fog
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
UNITY_FOG_COORDS(1)
float4 vertex : SV_POSITION;
float4 vertexW : TEXCOORD2;
float3 normalW : TEXCOORD3;
};
sampler2D _MainTex;
float4 _MainTex_ST;
float4 _BaseColor;
// ゲルストナー波
void gerstnerWave( in float3 localVtx, float t, float waveLen, float Q, float R, float2 browDir, inout float3 localVtxPos, inout float3 localNormal ) {
browDir = normalize( browDir );
const float pi = 3.1415926535f;
const float grav = 9.8f;
float A = waveLen / 14.0f;
float _2pi_per_L = 2.0f * pi / waveLen;
float d = dot( browDir, localVtx.xz );
float th = _2pi_per_L * d + sqrt( grav / _2pi_per_L ) * t;
float3 pos = float3( 0.0, R * A * sin( th ), 0.0 );
pos.xz = Q * A * browDir * cos( th );
// ゲルストナー波の法線
float3 normal = float3( 0.0, 1.0, 0.0 );
normal.xz = -browDir * R * cos( th ) / ( 7.0f / pi - Q * browDir * browDir * sin( th ) );
localVtxPos += pos;
localNormal += normalize( normal );
}
v2f vert (appdata v)
{
v2f o;
o.vertexW = mul( unity_ObjectToWorld, v.vertex );
float3 oPosW = float3( 0.0, 0.0, 0.0 );
float3 oNormalW = float3( 0.0, 0.0, 0.0 );
float t = _Time.y;
gerstnerWave( o.vertexW, t + 2.0, 0.8, 0.7, 0.3, float2( 0.2, 0.3 ), oPosW, oNormalW );
gerstnerWave( o.vertexW, t, 1.2, 0.3, 0.5, float2( -0.4, 0.7 ), oPosW, oNormalW );
gerstnerWave( o.vertexW, t + 3.0, 1.8, 0.3, 0.5, float2( 0.4, 0.4 ), oPosW, oNormalW );
gerstnerWave( o.vertexW, t, 2.2, 0.4, 0.4, float2( -0.3, 0.6 ), oPosW, oNormalW );
o.vertexW.xyz += oPosW;
// 座標変換
o.vertex = mul( UNITY_MATRIX_VP, o.vertexW );
o.uv = TRANSFORM_TEX( v.uv, _MainTex );
o.normalW = normalize( oNormalW );
UNITY_TRANSFER_FOG( o, o.vertex );
return o;
}
fixed4 frag (v2f i) : SV_Target
{
// sample the texture
fixed4 col = tex2D(_MainTex, i.uv);
float3 normalW = normalize( i.normalW );
// ディフューズ
float3 toLightDirW = normalize( _WorldSpaceLightPos0.xyz );
float diffusePower = dot( normalW, toLightDirW );
col.rgb = max( 0.0, diffusePower ) * _BaseColor.rgb * col.xyz;
// スペキュラ
float3 vertexToCameraW = normalize( _WorldSpaceCameraPos - i.vertexW.xyz );
float3 specularColor = pow( max( 0.0, dot( reflect( -toLightDirW, normalW ), vertexToCameraW ) ), 4.0f );
col.rgb += specularColor * 0.5f;
UNITY_APPLY_FOG( i.fogCoord, col );
return col;
}
ENDCG
}
}
}
一つのゲルストナー波の頂点位置と法線を算出してくれる「gerstnerWave関数」がこのシェーダの中核です。
// ゲルストナー波
void gerstnerWave(
in float3 localVtx,
float t,
float waveLen,
float Q,
float R,
float2 browDir,
inout float3 localVtxPos,
inout float3 localNormal
);
引数の意味は以下の通りとなっています:
localVtx: 元の頂点位置(ワールドにある平面メッシュの頂点座標)
t: 経過時間(秒)
waveLen: 波長(m)
Q: ゲルストナー波としての尖り度(0~1)。0にすると完全なsin波に、1にすると自然の限界に近い尖りになります。
R: 波の高さの調節項(0~1)。0だと完全フラット、1だと限界に近い波高になります。
browDir: 波が進む方向ベクトル
localVtxPos: (出力)localVtx位置を原点とした頂点の移動位置ベクトル。このベクトルを波の数だけ足して、元の頂点に足し算します。
localNormal: (出力)法線ベクトル。正規化されています。
頂点シェーダ内ではテストとして4本のゲルストナー波を発生させて合成しています:
o.vertexW = mul( unity_ObjectToWorld, v.vertex );
float3 oPosW = float3( 0.0, 0.0, 0.0 );
float3 oNormalW = float3( 0.0, 0.0, 0.0 );
float t = _Time.y;
gerstnerWave( o.vertexW, t + 2.0, 0.8, 0.7, 0.3, float2( 0.2, 0.3 ), oPosW, oNormalW );
gerstnerWave( o.vertexW, t, 1.2, 0.3, 0.5, float2( -0.4, 0.7 ), oPosW, oNormalW );
gerstnerWave( o.vertexW, t + 3.0, 1.8, 0.3, 0.5, float2( 0.4, 0.4 ), oPosW, oNormalW );
gerstnerWave( o.vertexW, t, 2.2, 0.4, 0.4, float2( -0.3, 0.6 ), oPosW, oNormalW );
o.vertexW.xyz += oPosW;
頂点位置のズレ(oPosW)は関数内部で足し合わされるようにしてあるので、最後にそのベクトルを元の頂点位置に足し算するだけでOKです。波のパラメータは至って適当ですが、波長1m前後の物を2本、2m前後の物を2本としてみました。経験則ですが、似たような波長を最低2本、異なる波長を2種類以上設定しないとあまり良い感じになりません。
フラグメントシェーダは単純にライティングしているだけなので説明は割愛します。
上のシェーダを実際にUnity上で実行してみたのが以下の動画です:
単純なライティングしかしていないのですが、しっかりうねってますよね~(^-^)
という事で、頂点を直接動かすゲルストナー波についてはこの位で十分かなと思います。ここまででテクスチャベースの波と頂点ベースの波、両方を見てきました。後は実際の波の見た目に近付ける作業となります。