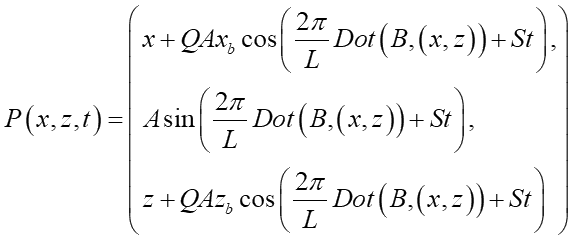
その9 波:ゲルストナー波でプレートをうねらす
前章で平面プレートの頂点の高さを頂点シェーダ内で直接計算してsin波を起こしてみました。しかし、sin波は丸っこい波なので実際の海などの波とはちょっと形が異なります。実際の海の波はその5「波頭は尖る!」の冒頭の写真にあるように結構尖っているんです。その5ではそれを実現するためにべき乗sin波及びトロコイド波を紹介しました。
この章で紹介するゲルストナー波も波頭を尖らせる事が出来ます。実はゲルストナー波はトロコイド波の仲間なのですが、ここでは区別して紹介したいと思います。
① ゲルストナー波はローカルの頂点を水平にも動かす!
前章のsin波は平面の頂点を高さ方向にだけ移動させて実現していました。実際もし波を構成する水が縦方向にしか移動しない性質だとすると、その波はsin波になるそうです。しかし、実際の水は波の下で回転運動を起こします。つまり水の位置が水平方向にも移動するんです。この水の性質をモデル化したのがゲルストナー波で、以下の式で表されます:
ちょっと何言ってるかわかんない式に見えますがw、ごちゃごちゃした記号をぎゅっとまとめると次のように簡略した見た目になります:
sin,cosの中は全部同じなのでθxzとしてしまいます。こうするとスッキリです。この式のx,zにはある水平座標が入ります。もしRxとRzが共にゼロだったら、計算後のx'、z'はx,zと同じ座標になります。そしてその時の波の高さHはsin波です。こういう場合は上の式は前章のsin波と同じ形になります。所が、RxとRzがゼロではない場合、(x,z)を与えると(x',z')はちょっとズレた座標になります。元の座標が水平方向に移動している状態です。その移動先座標の波の高さはsin波で計算されるのは変わりません。
つまりゲルストナー波は元の座標を意図的に揺らす事でsin波を変形させ尖らせているんです。実際QA=0.2、L=2、B=(1,0)、S=0として上の式のx'成分の式と高さHのグラフを描いてみるとこうなります:
赤丸の尖っている所がきゅっと点が詰まっているのが分かると思います。x成分が等間隔になっていないためです。これをその7で作成したメッシュプレートに適用するのが本章の目的です。
② 振幅Aと移動速度係数Sを波長Lで表現する
その4でも導いたのですが、海などの波は波長Lに対して振幅Aは最大でも1/14程度になる事が分かっています。また波頂の移動速度係数Sも波長Lと重力加速度gと関係している事が知られています。よって振幅Aと移動速度Sは波長Lで表現する事が可能です。
まずはAから。最大で波長の1/14なのでこうなります:
まぁこうですよね(^-^;。
移動速度v(係数Sではなくて)は重力加速度gから次式で算出されます:
1秒間でv(m)だけ進むという事です。今波長はL(m)ですから、その分だけ波が進行するのにかかる時間は、
である事が分かります。ここで①の波の高さの算出式をもう一度見てみましょう:
このsin関数の中身の内積がある項は(x,z)の地点が一定ならば時間tによらず一定です。つまりこの波の周期は第2項目のStのSの値で完全に制御される事になります。今波長Lの波が1周するのにかかる時間はsでした。s秒でStは2πになる…これは、
という事で、結局速度vと同じ式になってしまいました。
振幅Aと速度係数Sを波長Lで置き換える事が出来ましたので、置き換え版のゲルストナー波の式を以下に示します:
θがちょっとこちゃっとしていますが、座標Pの式自体は非常にシンプルですよね。波の高さを微調整するためにRという係数を追加しました。Rは0〜1までを取り、0だと全く波が立たない状態、1だと最高潮になります。何度か出てきている「波やべぇ係数」ですw。Qも0〜1の範囲で、0だとsin波、1だと自然の波の限界位の高さのゲルストナー波になります。
③ ゲルストナー波の法線
前章でsin波に陰影をつけるため法線を求めたように、ゲルストナー波も法線を求めなければ陰影が付きません。前章での法線の式を上のゲルストナー波の式に当てはめるとこうなります:
この偏微分の部分は、以下のように分解可能です:
「やめてぇ〜〜」っと目がくるくるしてしまうかもしれませんが(^-^;、微分はこういう分数みたいな関係が成り立つんです。一番右側に含まれる個々の偏微分は以下のような式になります:
これを先のHの偏微分の式に代入してあれこれ整理すると最終的にこうなりました:
これで法線Nが具体的にダイレクトに求まります。
①の最後に示した波長Lに基づくゲルストナー波の式と、上で求めた法線をその7で用意した空っぽシェーダの頂点シェーダ部分に書き込んでみます:
v2f vert (appdata v)
{
v2f o;
...
// ゲルストナー波
const float pi = 3.1415926535f;
const float grav = 9.8f;
float _t = 0.0f;
float _waveLen = 0.2f;
float _Q = 1.0f;
float _R = 1.0f;
float A = _waveLen / 14.0f;
float3 _browDir = normalize( float3( 0.4f, 0.0f, 0.7f ) );
float _2pi_per_L = 2.0f * pi / _waveLen;
float d = dot( _browDir.xz, v.vertex.xz );
float th = _2pi_per_L * d + sqrt( grav / _2pi_per_L ) * _t;
float H = _R * A * sin( th );
float xd = v.vertex.x + _Q * A * _browDir.x * cos( th );
float zd = v.vertex.z + _Q * A * _browDir.z * cos( th );
v.vertex.xyz = float3( xd, H, zd );
// ゲルストナー波の法線
float dx = _browDir.x * _R * cos( th ) / ( 7.0f / pi - _Q * _browDir.x * _browDir.x * sin( th ) );
float dz = _browDir.z * _R * cos( th ) / ( 7.0f / pi - _Q * _browDir.z * _browDir.z * sin( th ) );
float3 normal = normalize( float3( -dx, 1.0f, -dz ) );
// 座標変換
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
UNITY_TRANSFER_FOG(o,o.vertex);
o.normal = UnityObjectToWorldNormal( normal );
return o;
}
で、このゲルストナー波シェーダをメッシュプレートにそのまま適用したのが下の画です:
尖ったゲルストナー波になりました〜〜。法線も大丈夫そうです。カメラを正射影にして遠近感を無くした状態でワイヤーフレームで真上から見てみると、
波の尖った所の頂点群がぎゅーっと寄っている様子が良く分かります。
この章ではゲルストナー波で尖った波を作る方法を見てきました。何だか数式が並んで辟易とする章でした(^-^;。前章とこの章で一つの波を作る事が出来るようになりましたが、これだけでは現実の波っぽくはなりません。テクスチャベースの波で行ったのと同様にジオメトリレベルの波もやはり複数波を起こして合成する事でより現実の波に近くなります。次の章はその「合成」のお話です。