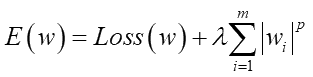
VisualStudio + Pythonでディープラーニング
過学習を防ぐ「正則化」とは？
(2019. 12. 30)
前の章でドロップアウトによって過学習を回避できる事を実験で試してみました。ドロップアウトは層に入ってくる入力値を一時的にゼロ化する事でデータの密度を疎にする処理でした。一方で本章で取り上げる「正則化（Regularization）」も同様に過学習を防ぐ手法の一つですが、その対象はデータではなく「推定値」です。「あえて推定の精度を下げる」という驚きの発想で過学習を防止します。いったいどういうからくりなのか、じっくり見ていきましょう。
① 評価関数にペナルティーを与える
ニューラルネットワークに限らずいわゆるフィッティングでは、一般にパラメータの数を増やしていくと当てはまりの指標である評価値をいくらでも小さくしていく事が出来ます。パラメータが多くなる程関数の形を自由に曲げる事ができるようになっていく（＝自由度が高くなっていく）からです。そういう過剰なパラメータによって学習データに沿い過ぎてしまい汎用性を失っているのが過学習を起こしたモデルです。これを解消するにはパラメータの数を減らせば良いのですが、沢山あるパラメータのどれを減らせば良いかなんて、何らかの統計学的な根拠が無い限り人が勝手に判断出来る物ではありません。ましてニューラルネットワークで用いられる何千何万というパラメータを手作業で選別する事は不可能です。
そこで次のように考えます。「パラメータが沢山ある事は良くない、すなわち低評価だ」と。そこから「基本的に評価値でフィッティングの良さを判断するけど、パラメータが多い場合は評価を下げる（＝評価値を増やす）」と発想すると、これまでに変わる新しい評価の考え方に辿り着けます。それを式で表したのが以下です：
Lossが評価関数で、通常はこれを最小にするパラメータwを探します。そこにパラメータの絶対値を何乗かした値の合計値を足し込み、それをλでスケーリングします。このλの値が0ならパラメータの事は無視した従来の評価値になりますし、0より大きくなればパラメータ全体の大きさが評価を下げる事になります。この評価に罰則を与える右辺第2項の事を「ペナルティー項」と言います。
もしLoss評価関数の値が同じであれば、ペナルティー項が小さいパラメータセットがより良いという事になります。もちろん小さいパラメータセットが必ずしも正義とは限りません。基本はフィッティングしていないと評価は下がる訳ですから。元のデータに寄り添いつつもより小さいパラメータ値を目指す。これにより程良くフィッティングされていくのです。
こういう「元の関数に対して追加の情報を与える事で新しい意味を見出したり曖昧さを解消したりする」事を正則化と言います。正則化は数学的にも良く研究されている大きな分野の一つです。では、ニューラルネットワークに用いられている過学習を防ぐ正則化の幾つかを紹介します。
② L1正則化（LASSO）
上式のべき乗pには0以上の実数が入ります。これはハイパーパラメータになっていて人が判断して数値を決めます。じゃじゃあどんな値を入れるのさ、という話になりますが、これにはいくつか代表値があります。その代表値のうちp=1のものを「L1正則化」と言います：
これは別名LASSO（Least Absolute Shrinkage and Selection Operator）とも呼ばれています。この英語名の日本語訳は定まっていないようですが、Shrinkage（圧縮）とSelection（選択）というワードにあるように、この正則化にはパラメータを選択しパラメータの数を減らす（次元圧縮）効果があります。なぜそうなるかはすごーく濃ゆい話になるので後述します。ちなみにL1の"L"はLASSOの"L"ではなくて、調べた範囲ですが数学者Henri Labesqueの名前が付いたLabesque空間（Labesque spaces）から来ているようです。
L1正則化を使うとあまり役に立っていないパラメータwが積極的にゼロ（無効化）へ追いやられ、意味の強いパラメータだけが残っていきます。これにより実質的なパラメータ数が減ります。これを「モデルがスパース（疎）になる」などと言います。疎になったモデルは細かい部分の表現力が下がるため、全体的に柔らかい形状になり過学習状態を脱せます。その性質からノイズを除去して大切な所を浮き彫りにする正則法として良く使われています。
③ L2正則化（Ridge）
べき乗値をp=2とするとL2正則化というものになります。別名Tikhonov正則化（Ridge正則化）とも言います：
L1正則化と違い、L2正則化はあまり役に立っていないパラメータも活用します。後述するイメージ図を見るとより鮮明にわかりますが、ざっくり言えば影響力の強いパラメータの効果を少し下げてその分細部の表現に回す働きをします。これにより過学習では無いけども細部もある程度再現するモデルとなります。そのためL1正則化によるモデルよりも精度が高いモデルになります。精度が高いというのはより優秀という事では無くて「細部が考慮されている」という意味です。
④ Elastic net正則化（L1/L2正則化）
L1正則化はパラメータを減らす、L2正則化は精度を上げる正則化でした。この両者の良い所取りをしたのがElastic net正則化です：
ペナルティー項がL1とL2の2つになっていて、それぞれを足し合わせています。λ1の値を増やせばL1正則化の効果が出てきて、λ2を増やすとL2正則化の効果が出てきます。双方の相対的な大きさで効果が変わります。
⑤ ハイパーパラメータλの値
上式のλは人が与えるハイパーパラメータの一つです。値を大きくするほど評価関数に対するペナルティーの効果が高くなるため重みwの値を全体的に小さくする作用が強くなっていきます。それは結果としてモデル全体の起伏を小さくしてしまうため、どんどんモデルが曖昧になってしまいます。つまり値が大きい程過学習から遠くなりますが、大き過ぎるとそもそもモデルとして使い物にならなくなっていきます。なので仮学習で程良い値に調整する必要があります。
⑤ KerasでのL1、L2正則化設定
Kerasには各層ごとにL1、L2及びL1L2正則化を設定できます：
model.add( keras.layers.Dense( units=100, activation="relu", kernel_regularizer=keras.regularizers.l1(0.01), input_shape=(1,) ) )
レイヤー作成時にkernel_regularizerに正則オブジェクトを渡します。デフォルトで作成可能な正則オブジェクトは以下の通りです：
keras.regularizers.l1(0.) #L1正則化
keras.regularizers.l2(0.) #L2正則化
keras.regularizers.l1_l2(l1=0.01, l2=0.01) #L1/L2正則化併用
引数はペナルティー係数λです。
という事で、ここまでが正則化の概要と良く利用される正則化のざっくりとした説明でした。効果を理解して使う分にはここまでのお話で事足ります。ただ色々な「何故？」が沢山あるこの正則化。ここから先はもう少し細かな数学的な背景について見ていきます。興味のある方だけどうぞ(^-^;
以下の理屈はopabinia2様の「機械学習に詳しくなりたいブログ」をはじめ様々なサイトの情報を参考にさせて頂きました。各サイト様誠にありがとうございますm(_ _)m
補足① 正則化とは？
私がこの章を書くにあたり、まず最初に思ったのは「正則って何？」でした。知らない立場からすると、意味を全然推測出来ない字面ですよね(^-^;。Wikipediaの「正則化」を見てみると、
数学・統計学・計算機科学において、特に機械学習と逆問題において、正則化（せいそくか、英: regularization）とは、不良設定問題を解いたり過学習を防いだりするために、情報を追加する手法である。モデルの複雑さに罰則を科すために導入され、なめらかでないことに罰則をかけたり、パラメータのノルムの大きさに罰則をかけたりする。
とあります。難しいワードが並んでいますが、正則化というのはどうやら「不良設定問題」を解く手法である、というのは読み取れます。で、その不良設定問題って何よ？という話です。これ、厳密さに目を瞑れば実は中学校の数学でもわかる割と簡単な事なんです(^-^)
いきなりですが次の連立方程式を解いてみましょう：
これは簡単ですよね。2つ目の式を-2倍して上の式と足し算すると y = 8 が出てきて、それを2つ目の式に代入すれば
x = -10が算出できます。このように解が一意に定まるような問題を「良設定問題（well-posed problem）」と言います。そして解が一意に定まる事を「正則である」と言います。
では上みたいな連立方程式で式が2本あれば常に解が求まるかというと、必ずしもそうとは限りません。次の連立方程式を見て下さい：
先程と同様に2つ目を-2倍して上の式と足すと…あれれ、xとyが両方打ち消されて消えてしまいます。じゃじゃあ2つ目から
y = 2 - x としてそれを上の式に代入しても…やっぱりxも同時に消えてしまいます。何故おかしな事になってしまうのか？それは式が2つあるように見えて実は1つしか無いからです。上の式の両辺を2で割ると下の式と一緒になってしまいますよね。このx
+ y = 2を満たすxとyの組み合わせは無限にあります。解が一意に定まらないので「正則では無い」のです。そしてこういう解が一意に定まらない問題の事を「不良設定問題」と言います。
上のような不良設定問題になっている連立方程式はそのままでは解が定まりません。でも、もし「x
= 3だよ」と追加の情報があったらどうでしょう。たちまち y = -1 と解けてしまいます。不良設定問題はそのままでは解が定まりませんが「x
= 3だよ」のように「情報を追加すれば」解けるようになる事があります。この「情報を追加する事で正則でない問題を解けるようにする事」を正則化と言います。
一方で、ニューラルネットワークではパラメータ推定は普通にできます。つまり元々の関数にちゃんと最適解が存在します。でも、この章でお話してきたようにその最適解が時に「望ましくない」のです（←過学習）。なので「ペナルティー項」という情報を追加して望ましい新たな解を求める関数を作りました。情報を追加する事で（望んでいる）解を求める事ができるようになるので、これも正則化と言えます。
補足② ラグランジュの未定乗数法
正則化についてイメージ出来た所で、冒頭で出てきた正則化の式をもう一度見てみます：
このE(w)を最小にするような重みwが望む解です。つまりこれは「最小化問題」になっています。ただ、元々のLoss(w)も最小なのがエライという最小化問題でした。この元の最小化問題から見るとペナルティー項は「制約」になっています。このような「ある制約の中で最小（最大）となるパラメータを求める」というのは「制約条件付き最適化問題」と呼ばれています。その制約条件付き最適化問題を解く手法として大変良く知られているのがラグランジュの未定乗数法です。これについては〇×的数学のお部屋その２「極値を求めるラグランジュの未定乗数法」で詳しく説明しております。詳しくはリンク先の章をご覧頂くとして、解く筋道をざっとおさらいします。
パラメータxの動ける範囲である制約条件をg(x)=0とし、これとf(x)とで次のような新しい関数を作ります：
この式はラグランジュの式と呼ばれます。λは制約条件を伸び縮みさせるスケール値です（意味合いについては先のリンク先で説明しています）。この関数F(x)をxとλそれぞれで偏微分し、その値がゼロであるという連立方程式を作ります：
この微分式は未知の変数がxとλ、式の本数も2本なので（双方が異なる式になっていれば）xもλも一意に求める事が出来ます。そして、そこで求めたxが制約条件を満たした中でのf(x)の極値（極小or極大）になります。「は？なんで！？」と思った方は「極値を求めるラグランジュの未定乗数法」をご覧ください(^-^;。理屈はさて置きそういう制約下の極値を求める事自体は簡単です。
補足③ ラグランジュの未定乗数法に沿った正則の式
補足②での元関数f(x)をLoss関数とし、制約条件として次のようなg(x)を考えます：
これは求めるパラメータの合計値をμ倍した値が高々1になる、というような制約条件です。制約条件が不等式になっています。こういうのを「不等式制約付き最適化問題」と言います。これについては「制約条件が不等式でのラグランジュの未定乗数法」に説明を上げました。大きく難しくなることは無くて、f(x)の極値がg(w)の内側にある場合は単なる制約なしの極値問題、外側にある場合はg(w)=0としたラグランジュの未定乗数法問題となります。ここからラグランジュの式を作ると、
こうなります。ここで、Loss関数はなるべく小さくなる（お椀の底を探す）目的なので、凸凹はしていますが基本下に凸の関数と言えます。そういう下に凸の関数の場合で極値がg(x)の範囲外にある場合、ラグランジュ式のλの値はゼロ未満のマイナス値になる事が知られています（KTT条件）。よって上の-λ'=λF（λF>0）と置き直すと、
このようにλの符号を反転出来ます（ただしλF>0）。この式、冒頭の正則化式E(w)と良く似ていますよね。
このF(w)の最小値を求めるにはパラメータwとλの偏微分がゼロとなるwやλを探します。同じように正則化式E(w)の最小値もその偏微分式がゼロとなるwを見つけます。そこで、両者の偏微分式を列挙してみます：
相当にそっくりです。唯一違うのが第2項の係数。上のラグランジュの式がλFμなのに対して下の正則化式はλのみです。そこで上の係数を一つにまとめてしまいましょう：
まったく一緒になってしまいました！これは「正則化式E(w)の極値問題は、g(w)≦0の制約条件下でのLoss関数の極値問題と一緒」という事を意味しています。ただちょっと注意があります。ラグランジュ式のλは未知数として推定する値です。一方で正則化式のλはハイパーパラメータとして人が与えます。「あれ？じゃぁ上と下のλは違う値になるんじゃ…？」と思いました、私は(^-^;。ここ、凄い悩んだ所です。これは次のような解釈でした。
上のラグランジュ式で推定されるのはλFです。それは確かに下の正則式で人が適当に与えたλとは異なります。でも、λFの値に対応するようにμの値を変えれば両者のλはいつも一緒に出来ます。ではμとは何だったか？
これは重みのべき乗の合計値が1/μ以下になるという範囲を表す値です。つまり、この正則化式E(w)での極値問題というのは、上のような制約範囲をλの値に対応するように大きくしたり小さくしたり自動的に調整して良い感じの落としどころを探ってくれているのです！なので、ハイパーパラメータとして与えているλの値が小さくなる程その逆数の関係になっている上の範囲は広くなります。ただ推定値であるλFは直接は分かりませんので、上のミューの範囲を直接意識する事はちょっと難しいかなと思います。だから仮学習でλの値を調整するテストをする必要があります。
補足④ L1正則化のイメージ
③まででこの正則式E(w)が上のg(w)≦0を制約条件としたラグランジュ式と一緒である事が分かりました。ではp=1の時のペナルティーであるL1正則化はどういう物になるかイメージしてみましょう。確かL1正則化は影響が小さいパラメータを取り除く効果があるのでした。なぜそうい事になるかもイメージを見ると分かります。人がグラフとして確認できるのは2変数までなので、重みw1、w2の2つで考えてみます。
Loss関数は下に凸の形状をしている（と考える）ので、(w1,w2)に対してプロットするとパラボラ的な形状になります。それに対してL1正則化の制約条件g(w)は次式のようになります：
これらをグラフにプロットすると次のようになります：
横軸がw1、縦軸がw2、3Dなグラフが元のLoss関数で、赤い四角枠がL1正則化の制約条件の範囲です。等高線はLoss関数の値を表しています。もし制約条件が無ければ等高線の円の中心がお椀の底なので、w1、w2はその辺りとして推定される事になります。しかしL1正則化の制約条件がある場合、w1、w2は赤い四角枠の内側でしか存在してはいけないので、図の緑の丸印の所が最小値として算出される事になります。この緑印でのw1の値がゼロになっているのに注目して下さい。等高線がw2軸に対しては垂直気味になっているのに対し、w1軸に対しては平行っぽくなっています。この為四角形の角が等高線に刺さるので、w2が採択されw1はゼロになる、という作用が起こります。これがL1正則化のパラメータ選択作用です。
もちろんお椀の底の位置によってはw1も採択される状況がありえます：
Loss関数の最小値が上図のような位置にある時、制約条件の四角い枠の辺の方が角よりも低くなります。この場合はw1もw2のどちらも非ゼロな値として採択されます。どちらもモデルに良く影響しているという事ですね。
ハイパーパラメータとして与えるλの値を小さくする、つまりペナルティーの効果を小さくすると、上の赤枠の範囲がどんどん広がっていきます。もしその範囲内にお椀の底が入ってしまうと、もはやペナルティー効果は失われてしまい,、パラメータの数によっては過学習化してしまう事になります：
なのでλの調整は正則化を使う場合には極めて重要です。しかしどういう範囲が適正であるかはモデルによって全く異なりますので、テスト学習を繰り返して調整する必要があります。
という事でニューラルネットワークの正則化のバックボーンについて少し深く掘り下げてみました。L1/L2正則化は基本的な物ではありますが、つくづく良く研究されているなぁと感心してしまいます。他にも様々な正則化が考案されています。その辺りはいずれまた(^-^;
